Интегральная функция распределения случайной величины и ее свойства
Для непрерывной случайной величины X вероятность 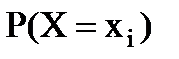
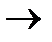 0, поэтому для нее удобнее использовать вероятность того, что случайная величина Х примет значение меньше х, где
0, поэтому для нее удобнее использовать вероятность того, что случайная величина Х примет значение меньше х, где 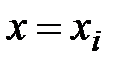 - текущее значение переменной. Эта вероятность
- текущее значение переменной. Эта вероятность 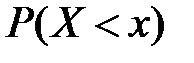 =
= 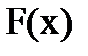 называется интегральной функцией распределения. Интегральная функция является универсальным способом задания случайных величин.
называется интегральной функцией распределения. Интегральная функция является универсальным способом задания случайных величин.
Свойства интегральной функции распределения:
1) 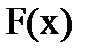 не убывающая функция, т. е. если
не убывающая функция, т. е. если 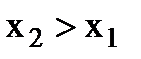 , то
, то 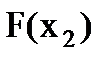
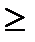
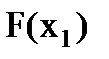 ;
;
2) 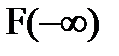 =0;
=0;
3) 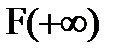 =1;
=1;
4) вероятность попадания случайной величины X в интервал а <Х< b: Р(а 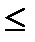 Х<b)=
Х<b)= 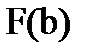 -
- 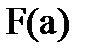 . (3.1)
. (3.1)
Вообще для непрерывных случайных вевичин верно: Р(а<Х<b)= Р(а 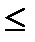 Х<b) =Р(а<Х
Х<b) =Р(а<Х 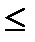 b)= Р(а
b)= Р(а 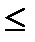 Х
Х 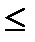 b).
b).
Дата добавления: 2015-08-11; просмотров: 989;
