Дисперсия дискретной случайной величины и ее свойства

Дисперсия служит для характеристики рассеяния случайной величины относительно ее математического ожидания и характеризует форму кривой распределения.

Дисперсией дискретной случайной величины X называется математическое ожидание квадрата отклонений случайной величины от ее математического ожидания:

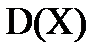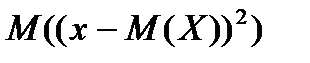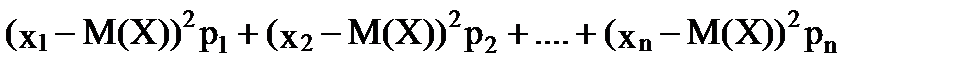= = . (2.8)

Свойства дисперсии:

1) D(С) = 0, где C=const;

2) D(CX)=C²D(X);

3) D(X)=M(X²)-(M(X))²,

где ;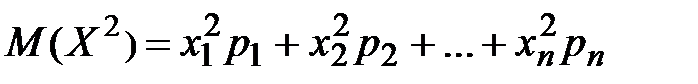

4) Если случайные величины X и Y независимы, то:

D(X 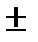Y)= D(X) + D(Y);

5) D(C+X)= D(X);

6) Для любых случайных величин Х и Y, D(X±Y)=D(X)+D(Y)±2cov(X,Y),

где cov(X,Y)=M((X-m_x)(Y-m_y)) - ковариация случайных величин X и Y (М(Х)= m_x, М(Y)= m_y).

Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания.

Дисперсия характеризует средний квадрат отклонения ДСВ, поэтому на практике часто используют в качестве характеристики разброса среднее квадратическое отклонение s(X)= 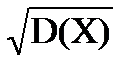, которое имеет ту же размерность, что и СВ Х.

Для распределения Бернулли: D(Х)=pq;

для биноминального закона: D(X)= npq, s(Х)= ;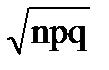

для геометрического закона и для геометрического закона+1: D(X)= ;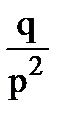

для отрицательного биномиального распределения:D(Х)= (кq)/(p²);

для гипергеометрического: D(X)= ;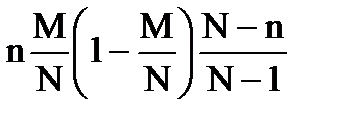

для распределения Пуассона: D(X)= l.

Только для распределения Пуассона M(X)=D(X) =l.