Одинаково распределенные взаимно-независимые случайные величины
Случайные величины называют одинаково распределенными, если они имеют одинаковые законы распределения. Поэтому у них совпадают числовые характеристики: математическое ожидание, дисперсия, среднее квадратическое отклонение.
Пусть X1, X2,…, Xn одинаково распределенные, взаимно независимые дискретные случайные величины, тогда: M(X1) = M(X2) = …= M(Xn) = M(X), D(X1) = D(X2) = …= D(Xn) = D(X).
Рассмотрим характеристики их средней арифметической 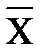 =
= 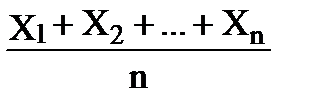 :
:
1) М( 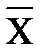 )=
)= 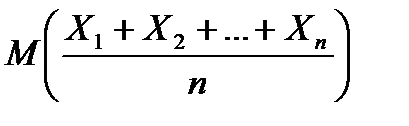 =
= 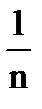 (M(X1) + M(X2) + …+ M(Xn))=
(M(X1) + M(X2) + …+ M(Xn))= 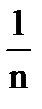 n M(X)= M(X);
n M(X)= M(X);
2) D( 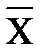 )=
)= 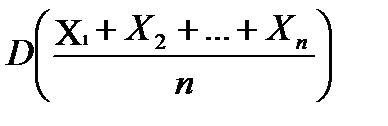 =
= 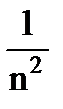 (D(X1) + D(X2) + …+ D(Xn))=
(D(X1) + D(X2) + …+ D(Xn))= 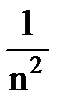 n D(X). D(
n D(X). D( 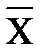 )=D(X)/n;
)=D(X)/n;
3) 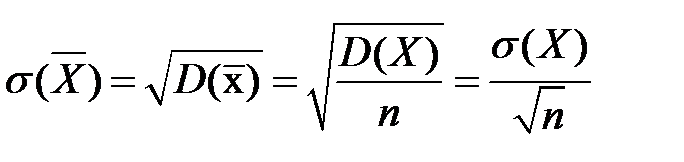 - стандартное отклонение среднего арифметического взаимно независимых одинаково распределенных случайных величин.
- стандартное отклонение среднего арифметического взаимно независимых одинаково распределенных случайных величин.
4) Дисперсияотносительной частоты 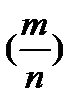 появления события А в n независимых испытаниях (в каждом из которых событие А появляется с вероятностью равной р, и не появляется с вероятностью q=1-p; m - число появлений события А в серии из n испытаний), равна D
появления события А в n независимых испытаниях (в каждом из которых событие А появляется с вероятностью равной р, и не появляется с вероятностью q=1-p; m - число появлений события А в серии из n испытаний), равна D 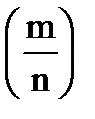 =
= 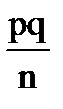 .
.
Дата добавления: 2015-08-11; просмотров: 1841;
