Нормальное распределение
Нормальное распределение играет исключительную роль в теории вероятностей. Это наиболее часто встречающийся закон распределения, главной особенностью которого является то, что он является предельным законом, к которому, при определённых условиях, приближаются другие законы распределения.
Дифференциальная функция нормального закона имеет вид:
f(x) = 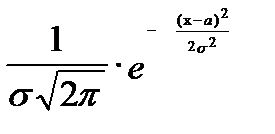 . (4.7)
. (4.7)
Числовые характеристики нормального закона:
1. Математическое ожидание характеризует центр распределения:
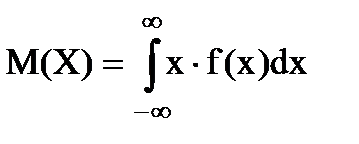 =
= 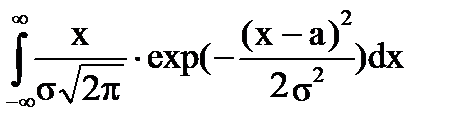 = а, где
= а, где 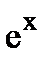 = exp (x);
= exp (x);
2. Дисперсия характеризует форму распределения:
D(X) = 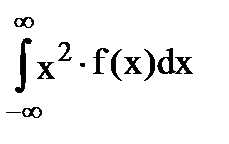 -(
-( 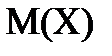 )2=
)2= 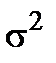 .
.
Свойства дифференциальной функции нормального закона:
1. Область определения: Df = R;
2. Ось 0X – горизонтальная асимптота;
3. x = а 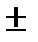 σ - две точки перегиба;
σ - две точки перегиба;
4. Максимум в точке с координатами: (а;  );
);
5. График симметричен относительно прямой x=а;
6. Вероятность попадания нормально распределенной случайной величины в заданный интервал определяется, по свойству интегральной функции:
Р( 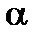 < x <
< x <  ) = Ф*
) = Ф* 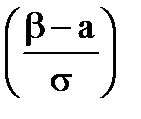 -Ф*
-Ф* 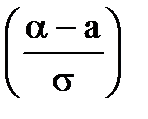 =Ф
=Ф 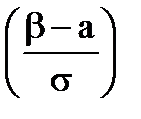 -Ф
-Ф 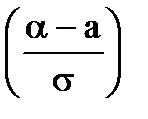 , где
, где
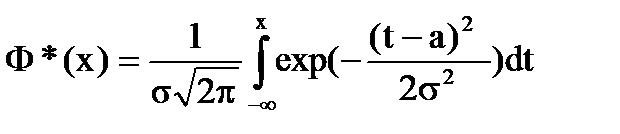 - (4.8)
- (4.8)
интегральная функция нормального закона; Ф(х)- функция Лапласа.
Вероятность заданного отклонения. Правило трех сигм. Найдем вероятность того, что случайная величина Х, распределённая по нормальному закону, отклонится от математического ожидания M(X)=a не более чем на величину e>0.
Р (| x – а| <e)= Р (-e< x – а < +e) = Р (а -e< x < а +e) =
= Ф* 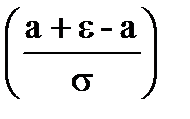 - Ф*
- Ф* 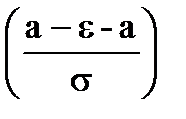 = Ф*
= Ф* 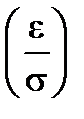 - (1-Ф*
- (1-Ф* 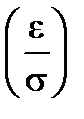 ) = 2Ф*
) = 2Ф* 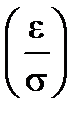 - 1
- 1
или используя функцию Лапласа:
P(|X-а|<e)=2Ф 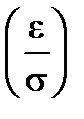 . (4.9)
. (4.9)
Найдём вероятность того, что нормально распределённая случайная величина X отклонится от M(X) = а на 3s:
Р(| x – а| < 3 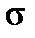 )= 2Ф
)= 2Ф 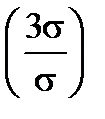 =2Ф(3)= 2×0,4965 = 0,9973.
=2Ф(3)= 2×0,4965 = 0,9973.
Отсюда следует правило 3s: если случайная величина X имеет нормальное распределение, то отклонение этой случайной величины от ее математического ожидания по абсолютной величине не превышает утроенное среднее квадратическое отклонение (3s).
4) Показательное распределение. Непрерывная случайная величинаХ, принимающая неотрицательные значения, имеет показательное распределение, если ее дифференциальная функция имеет вид

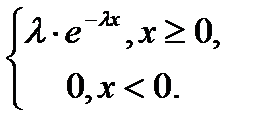 (4.10)
(4.10)
где 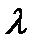 =const,
=const, 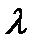 >0.
>0.
Интегральная функция показательного закона:
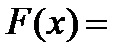
 (4.11)
(4.11)
Числовые характеристики показательного закона:
1. Математическое ожидание: 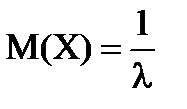 ;
;
2. Дисперсия: 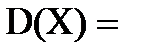
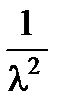 ,
,
3. Среднее квадратическое отклонение: s(Х)= 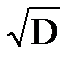 =
= 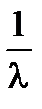 .
.
Вероятность попадания случайной величины Х в заданный интервал:
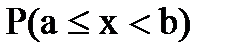 =
= 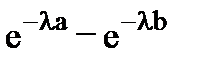 . (4.12)
. (4.12)
Показательное распределение играет большую роль в теории массового обслуживания (ТМО), теории надежности. В ТМО l - среднее число событий приходящихся на единицу времени. При определенных условиях, число событий, произошедших за промежуток времени t, распределено по закону Пуассона с математическим ожиданием а = lt. Длина промежутка t, между произвольными двумя соседними событиями, подчиняется показательному закону: P(T<t)=F(t)=1-elt .
Дата добавления: 2015-08-11; просмотров: 908;
