Закон распределения функции случайных величин.
Пусть имеется непрерывная случайная величина X с функцией плотности вероятности f(x). Другая случайная величина Y связана со случайной величиной X функциональной зависимостью: Y=φ(X). Случайная точка (X, Y) может находиться только на кривой y=φ(x).
Дифференциальная функция случайной величины Y определяется при условии, что φ(x) - монотонна на интервале (a, b), тогда для функции φ(x) существует обратная функция: φ-1=Ψ, х = Ψ(y).
Обычно числовая прямая разбивается на n промежутков монотонности и обратная функция находится на каждом из них, поэтому:
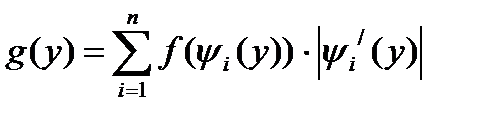 , (5.1)
, (5.1)
g(y) - дифференциальная функция случайной величины Y.
Математическое ожидание и дисперсию случайной величины Y – функции случайной величины X(Y=j(Х)), имеющей дифференциальную функцию f(x), можно определить по формулам:
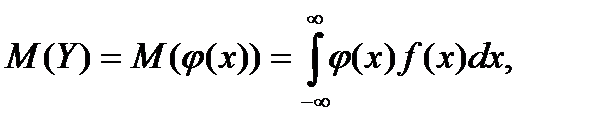 (5.2)
(5.2)
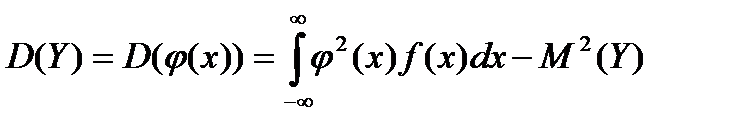 . (5.3)
. (5.3)
Пример. Случайная величина X подчиняется нормальному закону распределения с математическим ожиданием а и дисперсией s2, то есть дифференциальная функция имеет вид:
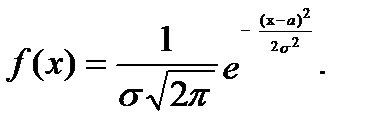
Найти дифференциальную функцию случайной величины Y=X2
Решение. На (0;¥) , для y=x2, обратная функция x=  = y1;
= y1;
на (- ¥;0) - обратная функция x= - 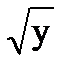 = y2 . По формуле (5.1):
= y2 . По формуле (5.1):
g(y)= 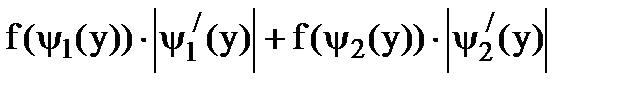 =
=
= 
При a=0 и s=1: 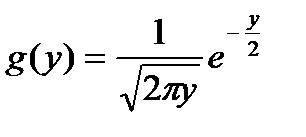 .
.
Дата добавления: 2015-08-11; просмотров: 811;
