Анализ устойчивости по критерию Найквиста.

Этот критерий основан на использовании амплитудно-фазовой частотной характеристики (АФЧХ) разомкнутой системы. Формально частотную передаточную функцию можно найти заменой переменной p на переменную jw.Разомкнем систему (место размыкания показано волнистой чертой на рисунок.4.). Передаточная функция разомкнутой системы имеет вид:

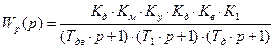
Все звенья разомкнутой системы устойчива, поскольку три звена имеют 3-й порядок, их характеристические коэффициенты положительны.

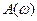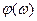Строим АФЧХ разомкнутой системы, рассчитываем значения и . Для упрощения расчетов пользуемся следующими правилами:

- модуль двойной части передаточной функции равен отношению модуля числителя к модулю знаменателя;

- модуль произведения равен произведению модулей;

- аргумент произведения равен сумме аргументов;

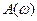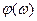Построим АФЧХ разомкнутой системы, рассчитав значения и .где 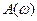-модуль частотной передаточной функции, 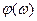-аргумент частотной передаточной функции

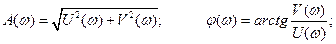
где 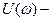вещественная часть частной передаточной функции

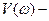мнимая часть

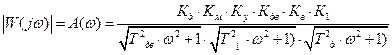
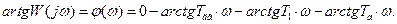
Для построения АФЧХ разомкнутой системы представим частотную передаточную функцию в виде:

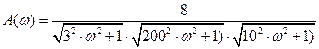
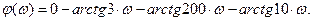
По этим выражениям, придавая 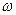значения от 0 до ∞, строим на комплексной плоскости АФЧХ разомкнутой системы (рис.5).

Пример расчета при 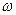=0,05. Воспользуемся формулами вышеизложенными.

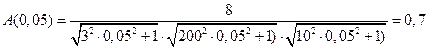
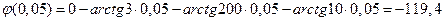
Таблица 2. – Результаты расчёта.

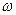
		0,001	0,005	0,008	0,01	0,03	0,05	∞
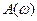
		7,84	5,65	4,22	3,56	1,25	0,2
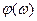
		-12	-48,7	-63,9	-70,8	-102,4	-119,4	-270

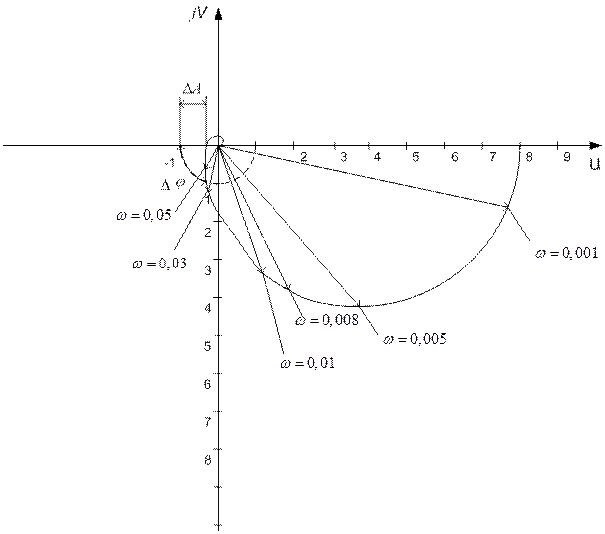
Рисунок.5. АФЧХ разомкнутой системы.