Системы с двумя входными воздействиями
Описание системы с двумя входными воздействиями
с использованием аппарата передаточных функций будет продемонстрировано на примере системы, структурная схема которой приведена на рис. 2.17.


В этой системе
· x(t) – основное или задающее входное воздействие;
· f(t) – суммарная помеха, приведенная к выходу дискриминатора;
· y(t) – выходная величина;
· e(t) = x(t) - y(t) – ошибка системы;
· W1(s) и W2(s) – заданные передаточные функции.
Пусть заданы система и оба входных воздействия. Чтобы описать свойства динамики системы требуется знать закон изменения выходной величины y = y(t) (или Y = Y(s)). Точность системы определяется ошибкой e(t) (или её изображением E(s)). Обе эти величины зависят от обоих входных воздействий. Для линейных непрерывных систем, учитывая принцип суперпозиции, указанная зависимость имеет вид
 ,
,
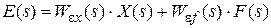 ; (2.63)
; (2.63)
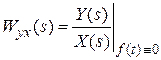 ,
,  ;
;
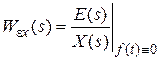 ,
, 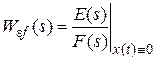 . (2.64)
. (2.64)
Требуется определить передаточные функции (2.64), являющиеся коэффициентами приведенной зависимости (2.63). Для этого воспользуемся методом стандартных соединений.
a). 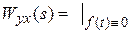 = ?
= ?
При отсутствии помехи f(t) структурная схема рассматриваемой системы совпадает со схемой рис. 2.15 при условии, что 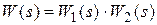 . Таким образом, в соответствии с формулой (2.61) получим
. Таким образом, в соответствии с формулой (2.61) получим
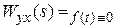 =
= 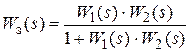 .
.
b). 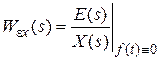 = ?
= ?


Отсутствует помеха f(t), выходная величина e(t). Схему системы удобно представить в виде, изображенном на рис. 2.18. В соответствии со схемой передаточная функция системы в разомкнутом состоянии
W(s) = 1, передаточная функция цепи обратной связи 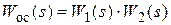 .
.
Таким образом,
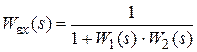 .
.
c).  = ?
= ?
В рассматриваемом случае структурная схема, изображенная на рис. 2.17, может быть преобразована и имеет вид стандартного встречно – параллельного соединения (см. рис. 2.19). При этом был применен приём, позволяющий переносить знак «-» через линейное звено.
 |
Следовательно,
 =
= 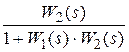 .
.
d).  = ?
= ?
При x(t) = 0 – ошибка системы e(t) = – y(t) и
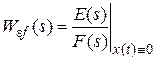 =
= 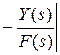 =
= 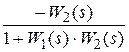 .
.
Дата добавления: 2015-07-30; просмотров: 781;
