Последовательное соединение элементов. На рис. 2.14 представлена схема последовательного соединения элементов.
На рис. 2.14 представлена схема последовательного соединения элементов.
Искомая передаточная функция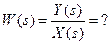 
В схеме три элемента, четыре переменные; x(t), y(t) – основные переменные, остальные – вспомогательные. Система уравнений в изображениях:
1. 
,
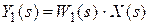2. 
,
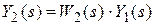3. 
.
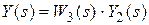Исключая вспомогательные переменные для искомой передаточной функции для трех элементов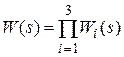 
и в общем случае для последовательного соединения n элементов получим:
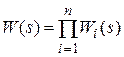. (2.58)
Комплесный коэффициент передачи соединения
.
, 
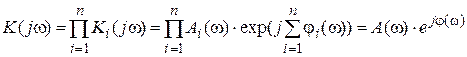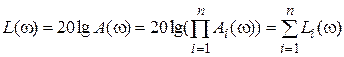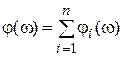. (2.59)
Таким образом, логарифмические частотные характеристики последовательного соединения элементов равно сумме логарифмических частотных характеристик его элементов.
2.5.1.3. Встречно – параллельное соединение элементов
На рис.2.15 представлена схема встречно - параллельного соединения элементов, в которой элемент с передаточной функцией W(s) охватывается отрицательной обратной связью. Чтобы показать это либо заштриховывается нижний сектор сумматора, либо (как это показано на рис. 2.14) около этого сектора ставится знак минус. Это означает, величина e(t) на выходе сумматора равна разности e(t) = x(t) – y1(t).
 |
В дальнейшем будут сохраняться обозначения и названия в этой схеме:
W(s) – передаточная функция прямой цепи,
Wос(s) – передаточная функция обратной связи,
Wз(s) – передаточная функция схемы в замкнутом состоянии,
x(t) – входное воздействие,
y(t) – выходная величина.
Искомая передаточная функция
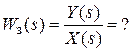
В схеме три элемента, четыре переменные; x(t), y(t) – основные переменные, e(t), y1(t) – вспомогательные. Система уравнений в изображениях:
1. 
,
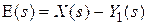2. 
,
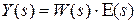3. 
.
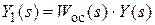Исключая вспомогательные переменные после некоторых преобразований получим:
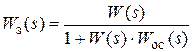. (2.60)
Дата добавления: 2015-07-30; просмотров: 587;