Сравнение свойств интегрирующего и инерционного звеньев

Анализ графических изображений характеристик инерционного звена (см. рис. 2.6, 2.7, 2.8) с аналогическими характеристиками идеальных усилительного и инерционного звеньев позволяет сделать следующие заключения о свойствах инерционного звена:

· в диапазоне малых частот (значительно меньших характерной для инерционного звена частоты ω = 1/T) инерционное звено обладает свойствами усилительного звена;

· в области больших частот (много больших частоты ω = 1/T) инерционное звено обладает свойствами интегрирующего звена;

· в диапазоне частот, отличающихся от частоты ω = 1/T в декады, инерционное звено обладает только ему присущими свойствами.

Особенно наглядно это можно продемонстрировать на примере сравнения логарифмических частотных характеристик (ЛАХ) рассматриваемых звеньев. действительно, на малых частотах характеристики инерционного звена 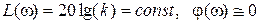, совпадают с аналогичными характеристиками усилительного звена. Набольших частотах асимптотическая логарифмическая характеристика как инерционного, так и интегрирующего звеньев имеет наклон -20 дБ/дек. И в том и другом случаях ϕ(ω) = -90^°.

Особый интерес представляет сравнение свойств интегрирующего звена (W(ω) = 1/ωT) и последовательности инерционных звеньев:

, , ,…, ,…,

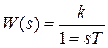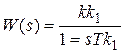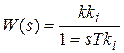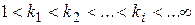. (2.48)

На рис. 2.10 приведены графики характеристик интегрирующего и инерционного звеньев. Следует отметить, что введение коэффициентов k_i изменяет характерные частоты инерционных звеньев, равных 1/Tk_i а частота ω = 1/T = k в этих условиях является коэффициентом усиления интегрирующего звена Сравнение изображений ЛАХ показывает, что в пределе, когда 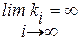, ЛАХ последовательности (2.48) инерционных звеньев в диапазоне частот около частоты ω = 1/T полностью совпадает с ЛАХ интегрирующего звена. Следовательно, должны совпадать в этом диапазоне и другие характеристики.

· Радиус полуокружности на графике АФХ инерционного звена когда 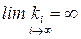стремится к бесконечности. Такая же ситуация должна наблюдаться и на графике АФХ интегрирующего звена. Считается, что на рис. 2.4 изображена только видимая часть характеристики. Полная АФХ интегрирующего звена должна быть дополнена дугой бесконечно большого радиуса так, чтобы при ω = 0 она начиналась на вещественной оси. Далее изображающая точка по дуге бесконечно большого радиуса по часовой стрелке перемещается на угол, равный 90^° и выходит на отрицательную часть мнимой оси и по видимой части характеристики при ω = 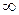приходит в начало координат.

· Как будет показано ниже, корни характеристического системы (или элемента системы) должны располагаться в левой полуплоскости комплексной плоскости. Мнимая ось является границей устойчивости. Корни 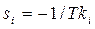звеньев последовательности (2.48) вещественные и устойчивые В пределе, когда , , 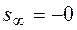т.е. бесконечно близко слева подходит к границе устойчивости, оставаясь в устойчивой области. Поэтому нулевой корень s = 0 интегрирующего звена считают условно устойчивым, но для этого дополняют область устойчивости около начала координат дугой бесконечно малого радиуса.

Итак, при наличии в передаточной функции системы (или элемента системы) интегрирующих звеньевеё АФХ дополняется дугой бесконечно большого радиуса, которая поворачивает конец видимой части АФХ против часовой стрелки на угол, равный девяноста градусам, помноженный на число интегрирующих звеньев.