Проективная плоскость и ее свойства. Модели проективной плоскости. Группа проективных преобразований. Применение к решению задач

При проектировании сохраняется прямолинейное расположение точек.

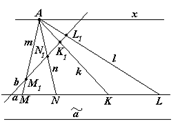
Дополним прямую точкой бесконечно удаленной 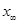, которую будем считать точкой соответствующей прямой х параллельной прямой а.

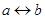взаимно-однозначное соответствие.

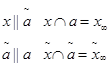
Прямая дополненная бесконечно удаленной точкой называется проективной прямой. Проективную прямую следует представлять в виде замкнутой линии.

Плоскость, дополненная бесконечно удаленной прямой называется проективной плоскостью. Пространство, дополненное бесконечно удаленной плоскостью называется проективным пространством.

Все параллельные прямые одного направления можно считать пучком прямых с общим несобственным центром, который проективным преобразованием легко можно перенести в обыкновенный пучок пересекающихся прямых. Все бесконечно удаленные точки лежат на бесконечно удаленной прямой.

Для построения модели проективного пространства можно взять всё множество векторов имеющих начало в одной точке и факторизовать его по отношению коллинеарности. Это отношение есть отношение эквивалентности. V/∆ – фактор-множество векторов по отношению их колленеарности. Получим множество классов этого фактор-множества, которое может служить для определения векторного пространства. Все модели проективных пространств изоморфны.

Проективные преобразования. Можно задать следующим образом: берём точку, которая в одном репере имеет некоторые координаты и ставим ей в соответствие точку, которая в другом репере имеет те же координаты. Такое отображение одной плоскости на другую плоскость оказывается взаимно-однозначным.

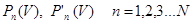
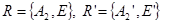
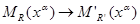– это отображение является биекцией (взаимно-однозначное).

Проективные преобразования пространства любой размерности образуют группу. Группа аффинных преобразований является подгруппой проективных преобразований.

Классическая проективная плоскость П определяется следующими аксиомами. Первые четыре из них являются обязательными.

1.Через две различные точки P и Q плоскости П проходит прямая, причём только одна.

2.Любые две прямые имеют общую точку.

3.Существуют три точки, не лежащие на одной прямой.

4.Каждая прямая содержит не менее трёх точек

Дополнительными аксиомами являются следующие:

5.Аксиома Дезарга. Если треугольники ABC и A’B’C' таковы, что прямые AA' , BB' и CC' пересекаются в точке O, то точки пересечения пар соответствующих сторон AB и A’B' (P), BC и B’C' (R), AC и A’C'(Q) лежат на одной прямой.

6.Аксиома Паппа. Если l и l' две различные прямые, A,B,С — три различные точки на прямой l, а A',B',C' — три различные точки l', причём все эти точки отличны от О — точки пересечения прямых l и l' , то точки пересечения пар соответствующих сторон AB' и A’B (P), BC' и B’C (R), AC' и A’C (Q) лежат на одной прямой.

7.Аксиома Фано. Пусть A, B, C, D — точки, никакие три из которых не лежат на одной прямой. Проведём все шесть прямых, соединяющих эти точки (AB, AC, AD, BC, BD, CD). Обозначим точку пересечения AB и CD через P, AC и BD через Q и AD и BC через R (диагональные точки). Эти диагональные точки не лежат на одной прямой.

Свойства:

1.Для любой проективной плоскости над телом выполняются аксиомы 1-4 и аксиома Дезарга. Обратно, если в плоскости П выполняется аксиома Дезарга, то она есть проективная плоскость над некоторым телом K.

2.Если выполняются аксиома Паппа и аксиомы 1-4, то выполняется и аксиома Дезарга. В этом случае П является проективной плоскостью над полем (то есть тело K коммутативно). Обратно, в любой проективной плоскости над полем выполняется аксиома Паппа.

3.Если выполняются аксиомы 1-4 и аксиома Дезарга, то аксиома Фано выполняется тогда и только тогда, когда П является проективной плоскостью над телом K характеристики ≠2.