Преобразования подобия и их свойства. Применение подобий к решению задач. Группа подобий и ее подгруппы

Подобием μ называется такое преобразование плоскости, которое расстояние между любыми двумя точками изменяет в r>0 раз: .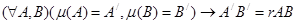

При условии r=1 это движение.

Гомотетия с коэффициентом 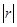также является частным случаем подобия .

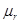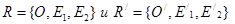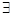Теорема: Если даны прямоугольные декартовы реперы , то единственное подобие μ, которое осуществляет перевод

Как и для движений можно показать, что 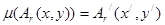и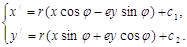

Из этих формул следует, что всякое подобие можно представить в виде произведения гомотетии и движения .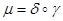

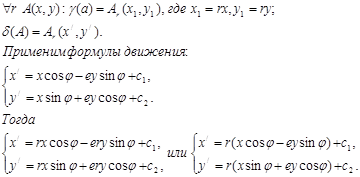
Из теоремы следует, что:

-прямые переходят в прямые,

-углы между линиями сохраняются,

-все расстояния изменяются в r раз.

Теорема: множество преобразований подобия (на плоскости) образуют группу.

Группу подобия G(μ) называют метрической группой (группой Клейна), которая позволяет измерять расстояния.

Подгруппой является группа движений 1 рода (не изменяет ориентацию фигуры: параллельный перенос, поворот, центральная симметрия и тождественное преобразование).

Подобие является частным случаем отношения эквивалентности:

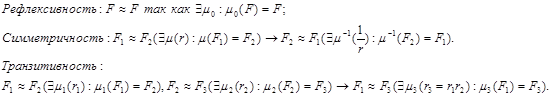
Подобие можно разбить на два класса:

-сохраняет ориентацию – 1 рода (образует группу);

-изменяет ориентацию – 2 рода (не образует группу).

При подобии площади фигур изменяются в r² раз, где r – коэффициент подобия.

Применение к решению задач:

Построить треугольник по двум углам и периметру.

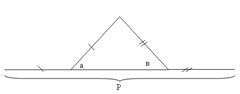
Используем свойство подобия: линейные размеры подобных фигур соотносятся с коэффициентом подобия r.

1.Строим треугольник, у которого:

-основание равно нашему периметру,

-углы при основании равны нашим углам (получим треугольник, подобный данному – согласно 2 признаку подобия);

2. Можно определить новый периметр K, исходный периметр и сторона AB известны.

Так как треугольники подобны, то 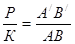. Согласно теореме Фалеса найдем .

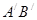Аналогично найдем .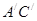

3. Откладываем 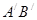от точки 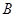и получаем 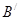, аналогично 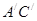от точки 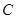и получаем 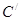. Строим углы a и b, и получаем нужный нам треугольник .