Трехмерное евклидово пространство. Скалярное произведение векторов, его свойства и применение к решению задач

В отличие от аффинного пространства в трехмерном евклидовом пространстве присутствуют такие фундаментальные понятия как: длина отрезка, длина вектора, угол между векторами, перпендикулярность и т. д.

Основными объектами являются векторы.

Основные отношения - сумма векторов, скалярное произведение, умножение вектора на число.

Аксиомы: аксиомы линейных векторов, аксиома размерности, аксиомы скалярного произведения.

Линейное векторное пространство называется евклидовым, если каждым двум векторам a и b этого пространства поставлено в соответствие число α, называемое скалярным произведением этих векторов.

Скалярным произведением ненулевого вектора а на ненулевой вектор b называется число (скаляр) равное произведению длин этих векторов на cos угла между ними (обозначения: ab, a*b, (ab)).

Т.о. аb=|a|*|b|*cos(a^b). (1)

Замечание: если хотя бы один из векторов a или b нулевой, то по определению ab=0.

Свойства скалярного произведения:

1)ab=ba -

2) (αa)b=α(ab) - для любого числа α

3)(a+b)c=ac+bc - для любых векторов a, b и с

4)если a≠0, то a²>0

Обозначение векторного евклидового пространства: Eⁿ

Обычное скалярное произведение в трёхмерном пространстве этим свойствам удовлетворяет. В этом случае определеное скалярное произведение, удовлетворяющее перечисленным свойствам, называется евклидовым пространством; оно может быть как конечномерным (n-мерным), так и бесконечномерным. Бесконечномерное евклидово пространство обычно называют гильбертовым пространством. Длина |x| вектора x и угол 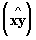между векторами х и у евклидова пространства определяются через скалярное произведение формулами

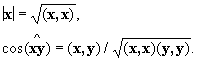
В евклидовых пространствах вводится понятие ортогональных (перпендикулярных) векторов. Именно векторы х и у называются ортогональными, если их скалярное произведение равно нулю: (х, у) =0.