Движения плоскости и их свойства. Примеры движений. Классификация движений. Группа движений. Применение движений к решению задач

Движение– это преобразования фигур, при котором сохраняются расстояния между точками. Если две фигуры точно совместить друг с другом посредством движения, то эти фигуры одинаковы, равны.

Движение– это биективное преобразование φ плоскости π, при котором для любых различных точек X, Y є π выполнено соотношение XY  φ(X )φ(Y).

Свойства движений:

1.Композиция φ ◦ ψ двух движений ψ, φ является движением.

Док-во: Пусть фигура F переводится движением ψ в фигуру F’, а фигура F’ переводится движением φ в фигуру F’’. Пусть при первом движении точка X фигуры F переходит в точку X’ фигуры F’ , а при втором движении точка X’ фигуры F’ переходит в точку X’’ фигуры F’’. Тогда преобразование фигуры F в фигуру F’’, при котором произвольная точка X фигуры F переходит в точку X’’ фигуры F’’, сохраняет расстояние между точками, а значит, также является движением.

Запись композиции всегда начинается с последнего движения, т.к. результатом композиции является конечный образ – он и ставится в соответствие исходному: X’’= ψ(X’) = ψ(φ (X)) = ψ ◦ φ (X)

2. Если φ – движение, то преобразование φ^-1 также является движением.

Док-во: Пусть преобразование фигуры F в фигуру F’ переводит различные точки фигуры F в различные точки фигуры F’. Пусть произвольная точка X фигуры F при этом преобразовании переходит в точку X’ фигуры F’.

Преобразование фигуры F’ в фигуру F, при котором точка X’ переходит в точку X, называется преобразованием, обратным данному. Для каждого движения φ можно определить обратное ему движение, которое обозначается φ^-1.

Т.о., преобразование, обратное движению, также является движением.

Очевидно, что преобразование φ^-1 удовлетворяет равенствам: f ◦ f^-1 = f^-1 ◦ f = ε, где ε – тождественное отображение.

3. Ассоциативность композиций: Пусть φ₁, φ₂, φ₃ – произвольные движения. Тогда φ₁◦(φ₂◦ φ₃) = (φ₁◦φ₂)◦φ₃.

Тот факт, что композиция движений обладает свойством ассоциативности, позволяет определить степень φ с натуральным показателем n.

Положим φ¹ = φ и φⁿ⁺¹ = φⁿ ◦ φ, если n ≥ 1. Таким образом, движение φⁿ получается путём n-кратного последовательного применения движения φ.

4. Сохранение прямолинейности: Точки, лежащие на одной прямой, при движении переходят в точки, лежащие на одной прямой, и сохраняется порядок их взаимного расположения.

Это значит, что если точки A, B, C, лежащие на одной прямой (такие точки называют коллинеарными), переходят в точки A₁, B₁, C₁, то эти точки также лежат на прямой; если точка B лежит между точками A и C, то точка B₁ лежит между точками A₁ и C₁.

Док-во. Пусть точка B прямой AC лежит между точками A и C. Докажем, что точки A₁, B₁, C₁ лежат на одной прямой.

Если точки A₁, B₁, C₁ не лежат на одной прямой, то они являются вершинами некоторого треугольника A₁B₁C₁. Поэтому A₁C₁ < A₁B₁ + B₁C₁.

По определению движения следует, что AC < AB + BC.

Однако по свойству измерения отрезков AC = AB + BC.

Мы пришли к противоречию. Значит, точка B₁ лежит между точками A₁ и C₁.

Допустим, что точка A₁ лежит между точками B₁, и C₁. Тогда A₁B₁ + A₁C₁ = B₁C₁, и, следовательно, AB + AC = BC. Но это противоречит равенству AB + BC = AC.

Т.о., точка A₁ нележит между точками B₁, и C₁.

Аналогично доказывается, что точка C₁ не можетлежать между точками A₁ и B₁. Т.к. из трёх точек A₁, B₁, C₁ одна лежит между двумя другими, то этой точкой может быть только B₁. Теорема доказана полностью.

Следствие. При движении прямая отображается на прямую, луч – на луч, отрезок – на отрезок, а треугольник – на равный ему треугольник.

Если через Х обозначить множество точек плоскости, а через φ(Х) - образ множества Х при движении φ, т.е. множество всех точек вида φ(х), где х є Х, то можно дать более корректную формулировку данного свойства:

Пусть φ – движение, А, В, С – три различные коллинеарные точки.

Тогда точки φ(А), φ(В), φ(С) также коллинеарны.

Если l – прямая, то φ(l) также прямая.

Если множество Х является лучом (отрезком, полуплоскостью), то множество φ(Х) также является лучом (отрезком, полуплоскостью).

5. При движении сохраняются углы между лучами.

Док-во. Пусть AB и AC – два луча, исходящие, из точки A, не лежащие на одной прямой. При движении эти лучи переходят в некоторые полупрямые (лучи) A₁B₁ и A₁C₁. Т.к. движение сохраняет расстояния, то треугольники ABC и A₁B₁C₁ равны по третьему признаку равенства треугольников (если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то эти треугольники равны).Из равенства треугольников следует равенство углов BAC и B₁ A₁C₁, что и требовалось доказать.

6. Всякое движение сохраняет сонаправленность лучей и одинаковую ориентированность флагов.

Лучи l_А и l_В называются сонаправленными(одинаково ориентированными, обозначение: l_А ↑↑ l_В), если один из них содержится в другом, или если они совмещаются параллельным переносом. ФлагF = (π_l, l_o) – это объединение полуплоскости π_l и луча l_o.

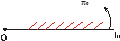
Точка О – начало флага, луч l_o с началом в точке О – древко флага, π_l – полуплоскость с границей l.

Док-во.Пусть φ – произвольное движение, l_А ↑↑ l_В –сонаправленные лучи с началами в точках А и В соответственно. Введём обозначения: l_А1 = φ(l_А), А₁ = φ(А), l_В1 = φ(l_В), В₁ = φ(А).Если лучи l_А и l_В лежат на одной прямой, то в силу сонаправленности один из них содержится в другом. Считая, что l_А  l_В , получаем φ(l_А)  φ(l_В), т.е. l_А1 ↑↑ l_В1 (символом  обозначается включение или равенство подмножества элементов множеству элементов).Если же l_А , l_В лежат на разных прямых, то пусть n = (AB).Тогда существует такая полуплоскость π_n, что l_А, l_В  π_n. Отсюда φ(l_А),φ(l_В) φ(π_n). Поскольку φ(π_n) – полуплоскость, причем ее граница содержит точки А₁ и В₁ , мы опять получаем, что l_А , l_В сонаправлены.

Применим теперь движение φ к одинаково ориентированным флагам F = (π_l,l_А), G = (π_m,m_B).Рассмотрим случай , когда точки A и B совпадают. Если прямые l и m различны, то одинаковая ориентированность флагов означает, что либо (1) l_А π_m,, m_А π’_l, либо (2) l_А π’_m, m_А π_l. Без ограничения общности можно считать, что выполняется условие (1). Тогда φ(l_А)  φ(π_m), φ(m_А)  φ(π’_l). Отсюда вытекает одинаковая ориентированность флагов φ(F) и φ(G).Если же прямые l, m совпадают, то либо F = G, либо F = G’. Отсюда следует, что флаги φ(F) и φ(G) одинаково ориентированные.

Пусть теперь точки A и B различны. Обозначим через n прямую (AB). Понятно, что найдутся сонаправленные лучи n_A и n_B и полуплоскость π_n такие, что флаг F₁ = (π_n, n_A) сонаправлен с F, а флаг G₁= (π_n, n_B,) сонаправлен с G. Значит φ(F) и φ(G) одинаково ориентированные.Теорема доказана.

Примеры движений:

1)параллельный перенос - такое преобразование фигуры, при котором все точки фигуры перемещаются в одном и том же направлении на одно и то же расстояние.

2)симметрия относительно прямой (осевая или зеркальная симметрия). Преобразование σ фигуры F в фигуру F’,при котором каждая её точка X переходит в точку X’, симметричную относительно данной прямой l, называется преобразованием симметрии относительно прямой l. При этом фигуры F и F’ называются симметричными относительно прямой l.

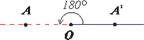
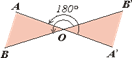
3)поворот вокруг точки. Поворотом плоскости ρ вокруг данной точки O называется такое движение, при котором каждый луч, исходящий из этой точки, поворачивается на один и тот же угол α в одном и том же направлении

4)скользящая симметрия (композиция осевой симметрии и параллельного переноса вдоль оси симметрии) – композиция движений τ ◦ σ_l, где σ_l – симметрия относительно прямой l, а τ – параллельный перенос вдоль прямой l, не являющийся тождественным отображением.

Классификация движений:

Теорема Шаля. Каждое движение первого рода является либо параллельным переносом, либо поворотом; каждое движение второго рода - либо осевая симметрия, либо скользящая симметрия.

Док-во. Пусть φ – произвольное движение первого рода. Можно считать, что φ ≠ ε. Множество I(φ) в этом случае либо пусто, либо одноэлементно. В первом случае φ – параллельный перенос, во втором – поворот.Пусть теперь φ – произвольное движение второго рода. Множество I(φ) в этом случае либо пусто, либо является прямой. Это означает, что φ либо скользящая симметрия, либо осевая симметрия. Теорема доказана.

Применение к решению задач:

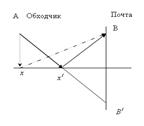
Задача1: Обходчику нужно выйти (из А) на железную дорогу (х) и дойти затем к почте (В) так, чтобы его путь был минимален.

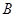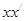Пунктиром обозначен произвольный путь (если точку х передвигать вдоль прямой). Если точку осевой симметрией ( через ось ) перевести в точку 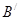, то 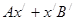будет минимальным. Таким образом точка 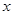должна стремиться в 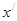. Путь 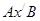- самый короткий.

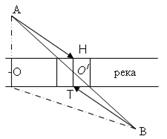
Задача 2: Пункты А и В находятся по разные стороны реки. Нужно построить мост через реку так, чтобы суммарное расстояние от пунктов А и В до моста было минимальное.

Пунктиром обозначен произвольный путь (он изменяется при движении точки О вдоль прямой 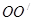). АВ – минимальное расстояние между А и В. Стрелками от А и В указан минимальный путь до мостов. Точка О должна стремиться к точке 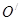. Путь 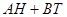к мосту от А и В минимален.