Формулы Сохоцкого
 Пусть
Пусть 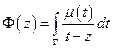 ,
, 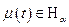
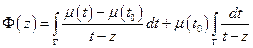
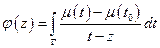 - непрерывна
- непрерывна
Поэтому
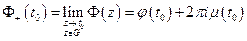
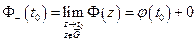
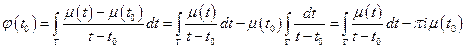
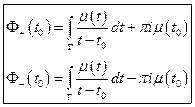
(интеграл существует в смысле главного значения, через предел)
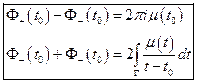
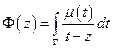
Вычеты
Опр. Пусть 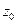 - изолированная особая точка функции
- изолированная особая точка функции 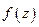 , возьмем окружность малого радиуса с центром в
, возьмем окружность малого радиуса с центром в 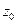 (
( 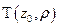 , чтобы внутри не было особых точек).
, чтобы внутри не было особых точек).
Тогда вычетом 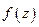 в
в 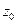 называется интеграл
называется интеграл
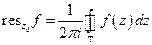
Если 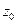 - устранимая особая точка, т.е.
- устранимая особая точка, т.е. 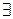 конечный предел
конечный предел 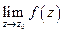 , то
, то
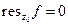
из теоремы Коши.
Если 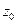 - особая (полюс, существенно особая) точка, то
- особая (полюс, существенно особая) точка, то 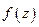 можно разложить в ряд Лорана, сходящийся в окрестности
можно разложить в ряд Лорана, сходящийся в окрестности 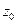
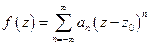
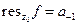
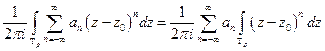
Все интегралы равны 0 кроме интеграла при 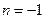
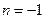 :
: 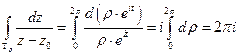
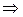
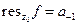
Дата добавления: 2015-07-24; просмотров: 1078;
