Формулы Сохоцкого ( - Племеля)
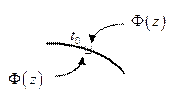 Рассмотрим предельные значения интеграла типа Коши при приближении к точке
Рассмотрим предельные значения интеграла типа Коши при приближении к точке 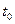 с разных сторон.
с разных сторон.
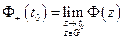
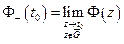
Пример: 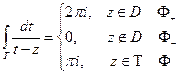
Формулы Сохоцкого связывают между собой 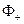 ,
, 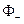 ,
, 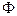 .
.
Теорема. Функция 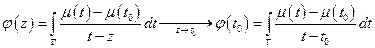 (непрерывная при
(непрерывная при 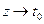 ,
, 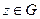 ,
, 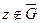 )
)
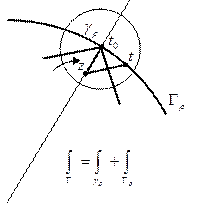
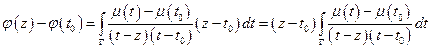
I.Пусть вначале 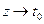 по некасательным направлениям к
по некасательным направлениям к 
Фиксируем малое 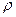
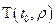
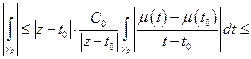
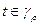 ,
, 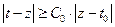
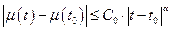
(Воспользуемся условием 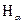
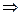 )
)

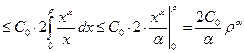
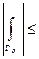 (возьмем
(возьмем 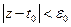 , чтобы
, чтобы 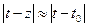 )
)
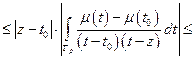
( 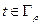 , то
, то 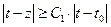 )
)
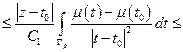
( 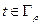 ,
,  ,
, 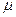 - непрерывна на
- непрерывна на  )
) 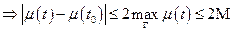
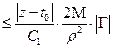
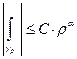
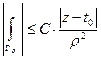
Вначале выбираем 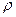 столь малым, чтобы
столь малым, чтобы 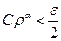
Затем выбираем 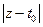 столь малым, чтобы
столь малым, чтобы 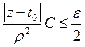
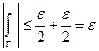 , ч.т.д.
, ч.т.д.
т. е. 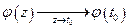 по некасательным путям.
по некасательным путям.
II.Надо избавится от стремления точки 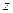 к точке
к точке 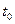 по некасательным путям
по некасательным путям
 Функция
Функция 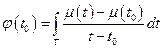 непрерывна по
непрерывна по 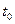 , т.к.
, т.к. 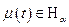
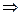

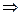 интеграл
интеграл 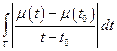
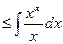 - сходится
- сходится 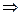
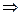 (по Т. Вейерштрасса)
(по Т. Вейерштрасса) 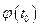 - непрерывна.
- непрерывна.
Пусть имеем 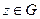 ,
, 
Пусть 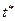 ближайшая к точке
ближайшая к точке 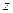 точка на кривой
точка на кривой 
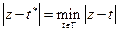
 Тогда
Тогда 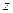 принадлежит углу с вершиной в точке
принадлежит углу с вершиной в точке 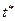 и величиной
и величиной 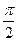
Если 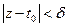 , то
, то 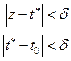
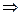
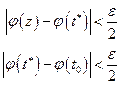
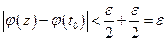
Дата добавления: 2015-07-24; просмотров: 1541;
