Гармонические функции
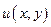 - гармоническая, если
- гармоническая, если 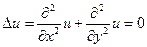 в
в 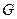 .
.
Если 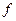 - аналитическая
- аналитическая  , то
, то 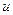 ,
, 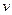 - гармонические
- гармонические
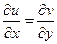 ;
; 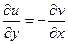
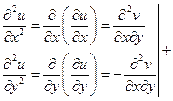
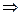
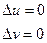
Справедливо обратное, если 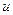 - гармоническая, то существует гармоническая
- гармоническая, то существует гармоническая 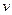 (которая называется сопряженной гармонической) так, что
(которая называется сопряженной гармонической) так, что 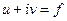 - аналитическая
- аналитическая 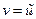 ,
, 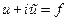 .
.
Доказательство: 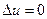
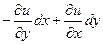 является полным дифференциалом некоторой функции
является полным дифференциалом некоторой функции 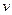 .
.
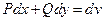
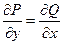
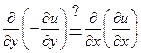 верно
верно 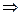
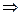
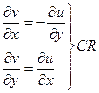
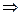
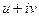 - аналитическая
- аналитическая
Функция 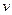 находится интегрированием
находится интегрированием
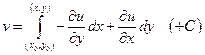
Дата добавления: 2015-07-24; просмотров: 596;
