Различные виды свойства линейности функции.

1)

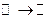
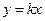
2)

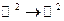
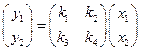
3) 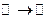(над полем 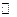) те же самые, что 2)

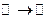(над полем )

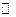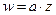
Пример: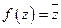

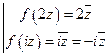
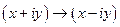
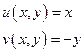
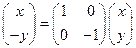
линейная на 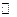, но не линейная на .

Таким образом получаем, что функция 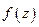дифференцируема тогда и только тогда, когда дифференциал 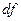является 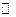-линейной функцией, т.е. ; .

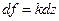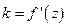Опр. Дифференцируемые функции в области называются аналитическими.

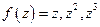- аналитические

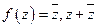- не аналитические

Примеры аналитических функций

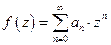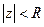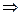
, ряд сходится при , 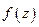- аналитическая в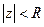

1) многочлены от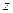

2) рациональные дроби от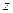

3)

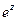
4)

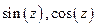
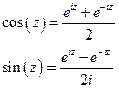
5)

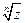
6)

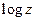
5),6) дифференцируемы там, где производная прямой функции не обращается в 0.

Полярная запись комплексного числа

,

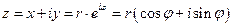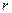- модуль комплексного числа, 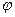- аргумент.

Чтобы определить обратную функцию к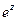

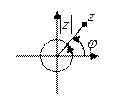
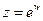. Зная 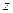, найти .

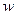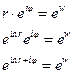
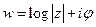
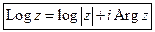- многозначная функция

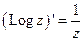- однозначная функция