Интеграл типа Коши

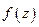 - аналитична в
- аналитична в 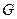 , с границей
, с границей 
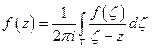 ,
, 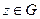
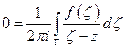 ,
, 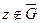
Пусть 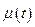 - функция, заданная на границе
- функция, заданная на границе  области
области 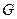 , непрерывна
, непрерывна
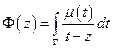 - интеграл типа Коши
- интеграл типа Коши
Утв. 1. Интеграл типа Коши 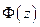 является аналитической функцией вне
является аналитической функцией вне  .
.
 Доказательство: Покажем, что
Доказательство: Покажем, что 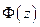 дифференцируема вне
дифференцируема вне  , т.е. показать, что существует предел
, т.е. показать, что существует предел 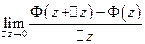 ,
, 
Формально продифференцируем
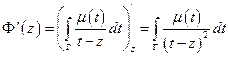 - интеграл существует
- интеграл существует
Значит надо показать, что:
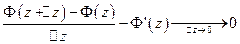
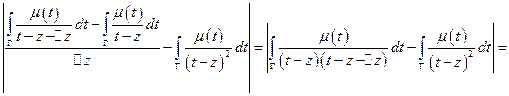
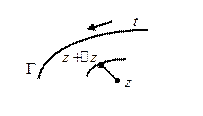
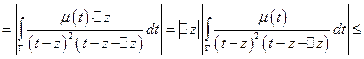
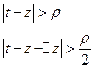
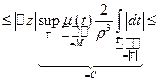
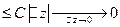
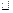
Какой смысл придать выражению?
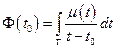 ,
, 
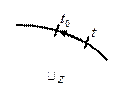 Данный интеграл не существует в обычном смысле
Данный интеграл не существует в обычном смысле

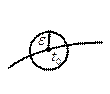 Часть
Часть  , которая не попадает в круг
, которая не попадает в круг 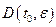 назовем
назовем 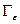
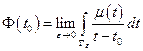
Если такого предела нет, то нет и интеграла типа Коши в 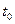 .
.
Для каких 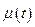 существует
существует 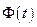 ?
?
Ответ: достаточно, чтобы 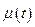 была непрерывна по Гёльдеру.
была непрерывна по Гёльдеру.
Опр. Функция 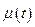 непрерывна по Гёльдеру с показателем
непрерывна по Гёльдеру с показателем 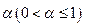 , если
, если 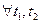
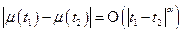
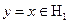 (условие Гёльдера с показателем 1)
(условие Гёльдера с показателем 1)
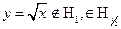
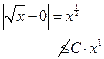 .
.
Если 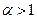 ,
, 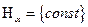 .
.
Теорема. Если 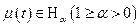 , то существует интеграл типа Коши
, то существует интеграл типа Коши 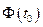 ,
,  .
.
Доказательство: Хотим показать, что существует интеграл и на границе
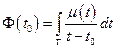
Возьмем кривую  , надо доказать, что существует предел (который указан выше)
, надо доказать, что существует предел (который указан выше)

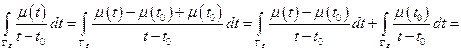
( 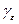 - часть окружности
- часть окружности 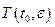 , которая не лежит в области
, которая не лежит в области 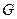 )
)
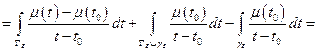
(применяем формулу Коши к интегралу по 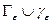 )
)
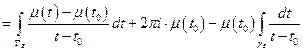
Докажем, что в обоих интегралах существует предел при 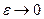 .
.
1) 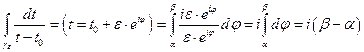 - величина угла, под которым часть окружности видна из точки
- величина угла, под которым часть окружности видна из точки 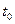 .
.
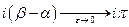
Если  - гладкая, то при
- гладкая, то при 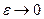 этот угол стремится к
этот угол стремится к 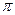 .
.
2) 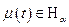
Тогда 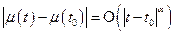
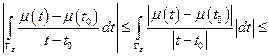
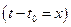
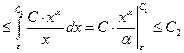
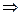 По признаку Вейерштрасса
По признаку Вейерштрасса 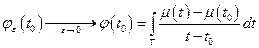
Для исходного интеграла имеем
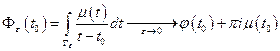 .
.
Значит
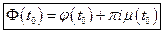
Дата добавления: 2015-07-24; просмотров: 996;
