Количественная мера неопределенности.
Пусть опыт имеет n равновероятных исходов.
Очевидно, что неопределенность каждого из них зависит от n, т.е. мера неопределенности является функцией числа исходов f(n).
Можно указать некоторые свойства этой функции:
1. f(1) = 0, поскольку при n = 1 исход опыта не является случайным и, следовательно, неопределенность отсутствует;
2. f(n) возрастает с ростом n, поскольку чем больше число возможных исходов, тем более затруднительным становится предсказание результата опыта.
Для определения явного вида функции f(n) рассмотрим два независимых опыта 
и 
с количествами равновероятных исходов, соответственно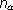 
, 
.
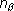(Для обозначения опытов со случайными исходами будем использовать греческие буквы , и т.д., а для обозначения отдельных исходов опытов (событий) – латинские заглавные A, B и т.д.)
Пусть имеет место сложный опыт, который состоит в одновременном выполнении опытов и ;
Число возможных его исходов равно 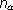· 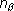, причем, все они равновероятны.
Очевидно, неопределенность исхода такого сложного опыта 
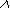
будет больше неопределенности опыта , поскольку к ней добавляется неопределенность ; мера неопределенности сложного опыта равна f( · ).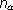
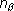С другой стороны, меры неопределенности отдельных и составляют, соответственно, f( 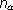) и f( ).
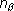В первом случае (сложный опыт) проявляется общая (суммарная) неопределенность совместных событий, во втором – неопределенность каждого из событий в отдельности.
Однако из независимости и следует, что в сложном опыте они никак не могут повлиять друг на друга и, в частности, не может оказать воздействия на неопределенность , и наоборот.
Следовательно, мера суммарной неопределенности должна быть равна сумме мер неопределенности каждого из опытов, т.е. мера неопределенности аддитивна:
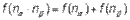(1.1)
Доказано, что единственная функцияf(n), из всех существующих классов функций удовлетворяющая свойствам (1) и (2) и соотношению (1.1) является log(n).
Таким образом: за меру неопределенности опыта с n равновероятными исходами можно принять число logа(n).
Выбор основания логарифма в данном случае значения не имеет, поскольку в силу известной формулы
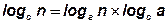
преобразования логарифма logа(n) от одного основания а к другому основанию с состоит во введении одинакового для обеих частей выражения (1.1) постоянного множителя logca, что равносильно изменению масштаба (т.е. размера единицы) измерения неопределенности.
Исходя из этого, мы имеет возможность выбрать из каких-то дополнительных соображений основание логарифма.
Таким удобным основанием оказывается 2, поскольку в этом случае за единицу измерения принимается неопределенность, содержащаяся в опыте, имеющем лишь два равновероятных исхода, которые можно обозначить, например, ИСТИНА (True) и ЛОЖЬ (False) и использовать для анализа таких событий аппарат математической логики.
Единица измерения неопределенности при двух возможных равновероятных исходах опыта называется бит
(Название бит происходит от английского binary digit, что в дословном переводе означает "двоичный разряд" или "двоичная единица".)
Таким образом, функция, описывающей меру неопределенности опыта, имеющего n равновероятных исходов, может быть представлена в виде:
f(n) = log2n (1.2).
Эта величина получила название энтропии. В дальнейшем будем обозначать ее H.
Вновь рассмотрим опыт с n равновероятными исходами.
Поскольку каждый исход случаен, он вносит свой вклад в неопределенность всего опыта, но так как все n исходов равнозначны, разумно допустить, что и их неопределенности одинаковы.
Из свойства аддитивности неопределенности (1.1), а также того, что согласно (1.2) общая неопределенность равна log2n, следует, что неопределенность, вносимая одним исходом составляет
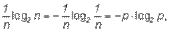
где
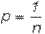
– вероятность любого из отдельных исходов.
Таким образом, неопределенность, вносимая каждым из равновероятных исходов, равна:
H = - p log2p (1.3).
Обобщим формулу (1.3) на ситуацию, когда исходы опытов не равновероятны, например, p(A1) и p(A2).
Тогда:
H1 = - p(A1) log2 p(A1) и H2 = - p(A2) log2 p(A2)
H = H1 + H2 = -p(A1) log2 p(A1) - p(A2) log2 p(A2)
Обобщая это выражение на ситуацию, когда опыт имеет n не равновероятных исходов A1, A2,..., An, получим:
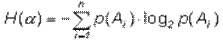(1.4)
Введенная таким образом величина, как уже было сказано, называется энтропией опыта .
Используя формулу для среднего значения дискретных случайных величин, можно записать:
H( ) = - log2 p (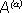 
),
где 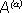– обозначает исходы, возможные в опыте .
Энтропия является мерой неопределенности опыта, в котором проявляются случайные события, и равна средней неопределенности всех возможных его исходов.
Для практики формула (1.4) важна тем, что позволяет сравнить неопределенности различных опытов со случайными исходами.
Пример. Имеются два ящика, в каждом из которых по 12 шаров.
- в первом – 3 белых, 3 черных и 6 красных;
- во втором – каждого цвета по 4.
Опыты состоят в вытаскивании по одному шару из каждого ящика.
Что можно сказать относительно неопределенностей исходов этих опытов?
Согласно (1.4) находим энтропии обоих опытов:
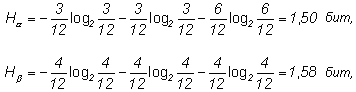
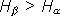, т.е. неопределенность результата в опыте выше и, следовательно, предсказать его можно с меньшей долей уверенности, чем результат .
Дата добавления: 2015-07-22; просмотров: 2624;