Информация и алфавит
Естественной для органов чувств человека является аналоговая форма представления информации, универсальной признано считать дискретную форму представления информации с помощью некоторого конечного набора знаков – алфавита.
Именно таким образом представленная информация обрабатывается компьютером, передается по компьютерным и иным линиям связи.
Сообщение есть последовательность знаков алфавита. При их передаче возникает проблема распознавания знака: каким образом прочитать сообщение, т.е. по полученным сигналам установить исходную последовательность знаков первичного алфавита.
В устной речи это достигается использованием различных фонем (основных звуков разного звучания), по которым мы и отличает знаки речи.
В письменности это достигается различным начертанием букв и дальнейшим нашим анализом написанного.
Появление конкретного знака (буквы) в конкретном месте сообщения – событие случайное. Следовательно, узнавание (отождествление) знака требует получения некоторой порции информации.
Можно связать эту информацию с самим знаком и считать, что знак несет в себе (содержит) некоторое количество информации. Оценим это количество.
Самое грубое приближение – нулевое (номер приближения отражается индексом у получаемых величин).
Предположим, что появление всех знаков (букв) алфавита в сообщении равновероятно.
Тогда количество знаков для английского алфавита - ne=27 (с учетом пробела как самостоятельного знака); для русского алфавита - nr=34. Из формулы Хартли находим:
I0(e) =log227 = 4,755 бит.
I0(r) =log234 = 5,087 бит.
Получается, что в нулевом приближении со знаком русского алфавита в среднем связано больше информации, чем со знаком английского.
Например, в русской букве "а" информации больше, чем в "a" английской!
Это, безусловно, не означает, что английский язык – язык Шекспира и Диккенса – беднее, чем язык Пушкина и Достоевского.
Лингвистическое богатство языка определяется количеством слов и их сочетаний, а это никак не связано с числом букв в алфавите.
С точки зрения техники это означает, что сообщения из равного количества символов будет иметь разную длину (и соответственно, время передачи) и большими они окажутся у сообщений на русском языке.
В качестве следующего (первого) приближения, уточняющего исходное, попробуем учесть то обстоятельство, что относительная частота, т.е. вероятность появления различных букв в сообщении различна.
Рассмотрим таблицу средних частот букв для русского алфавита, в который включен также знак "пробел" для разделения слов (из книги А.М. и И.М.Ягломов [с.238]);
с учетом неразличимости букв "е" и "ë", а также "ь" и "ъ" (так принято в телеграфном кодировании), получим алфавит из 32 знаков со следующими вероятностями их появления в русских текстах:
| Таблица 1. Частота появления букв Буква | Частота | Буква | Частота | Буква | Частота | Буква | Частота |
| пробел | 0,175 | o | 0,090 | е, ë | 0,072 | а | 0,062 |
| и | 0,062 | т | 0,053 | н | 0,053 | с | 0,045 |
| р | 0,040 | в | 0,038 | л | 0,035 | к | 0,028 |
| м | 0,026 | д | 0,025 | п | 0,023 | у | 0,021 |
| я | 0,018 | ы | 0,016 | з | 0,016 | ъ, ь | 0,014 |
| б | 0,014 | г | 0,013 | ч | 0,012 | й | 0,010 |
| х | 0,009 | ж | 0,007 | ю | 0,006 | ш | 0,006 |
| ц | 0,004 | щ | 0,003 | э | 0,003 | ф | 0,003 |
Для оценки информации, связанной с выбором одного знака алфавита с учетом неравной вероятности их появления в сообщении (текстах) можно воспользоваться формулой (1.14).
Из нее, в частности, следует, что если pi – вероятность (относительная частота) знака номер i данного алфавита из N знаков, то среднее количество информации, приходящейся на один знак, равно:
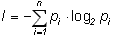 (1.17)
(1.17)
Это и есть знаменитая формула К.Шеннона, с работы которого "Математическая теория связи" (1948) принято начинать отсчет возраста информатики, как самостоятельной науки.
В нашей стране практически одновременно с Шенноном велись подобные исследования, например, и в том же 1948 г. вышла работа А.Н.Колмогорова "Математическая теория передачи информации".
Применение формулы (1.17) к различным алфавитам дает следующие значение средней информации на знак:
· алфавиту русского языка дает 1(r)= 4,36 бит,
· а для английского языка I1(e) = 4,04 бит,
· для французского I1(l) = 3,96 бит,
· для немецкого I1(d) = 4,10 бит,
· для испанского I1(s) = 3,98 бит.
Как мы видим, и для русского, и для английского языков учет вероятностей появления букв в сообщениях приводит к уменьшению среднего информационного содержания буквы, что, кстати, подтверждает справедливость формулы (1.7).
Несовпадение значений средней информации для английского, французского и немецкого языков, основанных на одном алфавите, связано с тем, что частоты появления одинаковых букв в них различаются.
В рассматриваемом приближении по умолчанию предполагается, что вероятность появления любого знака в любом месте сообщения остается одинаковой и не зависит от того, какие знаки или их сочетания предшествуют данному.
Такие сообщения называются шенноновскими (или сообщениями без памяти).
Сообщения, в которых вероятность появления каждого отдельного знака не меняется со временем, называются шенноновскими, а порождающий их отправитель – шенноновскимисточником.
Если сообщение является шенноновским, то набор знаков (алфавит) и вероятности их появления в сообщении могут считаться известными заранее.
В этом случае:
· с одной стороны, можно предложить оптимальные способы кодирования, уменьшающие суммарную длину сообщения при передаче по каналу связи.
· с другой стороны, интерпретация сообщения, представляющего собой последовательность сигналов, сводится к задаче распознавания знака, т.е. выявлению, какой именно знак находится в данном месте сообщения.
А такая задача, как мы уже убедились в предыдущем шаге, может быть решена серией парных выборов.
При этом количество информации, содержащееся в знаке, служит мерой затрат по его выявлению.
Последующие (второе и далее) приближения при оценке значения информации, приходящейся на знак алфавита, строятся путем учета корреляций, т.е. связей между буквами в словах.
Дело в том, что в словах буквы появляются не в любых сочетаниях; это понижает неопределенность угадывания следующей буквы после нескольких, например, в русском языке нет слов, в которых встречается сочетание щц или фъ.
И напротив, после некоторых сочетаний можно с большей определенностью, чем чистый случай, судить о появлении следующей буквы, например, после распространенного сочетания пр- всегда следует гласная буква, а их в русском языке 10 и, следовательно, вероятность угадывания следующей буквы 1/10, а не 1/33.
В связи с этим примем следующее определение:
Сообщения (а также источники, их порождающие), в которых существуют статистические связи (корреляции) между знаками или их сочетаниями, называются сообщениями (источниками) с памятью или марковскими сообщениями (источниками).
Как указывается в книге Л.Бриллюэна [с.46], учет в английских словах двухбуквенных сочетаний понижает среднюю информацию на знак до значения I2(e)=3,32 бит, учет трехбуквенных – до I3(e)=3,10 бит. Шеннон сумел приблизительно оценить I5(e)  2,1 бит, I8(e)
2,1 бит, I8(e)  1,9 бит. Аналогичные исследования для русского языка дают: I2(r) = 3,52 бит; I3(r)= 3,01 бит.
1,9 бит. Аналогичные исследования для русского языка дают: I2(r) = 3,52 бит; I3(r)= 3,01 бит.
Последовательность I0, I1, I2... является убывающей в любом языке.
Экстраполируя ее на учет бесконечного числа корреляций, можно оценить предельную информацию на знак в данном языке 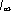 , которая будет отражать минимальную неопределенность, связанную с выбором знака алфавита без учета семантических особенностей языка, в то время как I0 является другим предельным случаем, поскольку характеризует наибольшую информацию, которая может содержаться в знаке данного алфавита.
, которая будет отражать минимальную неопределенность, связанную с выбором знака алфавита без учета семантических особенностей языка, в то время как I0 является другим предельным случаем, поскольку характеризует наибольшую информацию, которая может содержаться в знаке данного алфавита.
Шеннон ввел величину, которую назвал относительной избыточностью языка:
 (1.18)
(1.18)
Избыточность является мерой бесполезно совершаемых альтернативных выборов при чтении текста. Эта величина показывает, какую долю лишней информации содержат тексты данного языка; лишней в том отношении, что она определяется структурой самого языка и, следовательно, может быть восстановлена без явного указания в буквенном виде.
Исследования Шеннона для английского языка дали значение 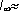 1,4÷1,5 бит, что по отношению к I0=4,755 бит создает избыточность около 0,68.
1,4÷1,5 бит, что по отношению к I0=4,755 бит создает избыточность около 0,68.
Подобные оценки показывают, что и для других европейских языков, в том числе русского, избыточность составляет 60 – 70%.
Это означает, что в принципе возможно почти трехкратное (!) сокращение текстов без ущерба для их содержательной стороны и выразительности.
Например, телеграфные тексты делаются короче за счет отбрасывания союзов и предлогов без ущерба для смысла; в них же используются однозначно интерпретируемые сокращения "ЗПТ" и "ТЧК" вместо полных слов (эти сокращения приходится использовать, поскольку знаки "." и "," не входят в телеграфный алфавит).
Однако такое "экономичное" представление слов снижает разборчивость языка, уменьшает возможность понимания речи при наличии шума (а это одна из проблем передачи информации по реальным линиям связи), а также исключает возможность локализации и исправления ошибки (написания или передачи) при ее возникновении.
Именно избыточность языка позволяет легко восстановить текст, даже если он содержит большое число ошибок или неполон (например, при отгадывании кроссвордов или при игре в "Поле чудес"). В этом смысле избыточность есть определенная страховка и гарантия разборчивости.
На практике учет корреляций в сочетаниях знаков сообщения весьма затруднителен, поскольку требует объемных статистических исследований текстов.
Кроме того, корреляционные вероятности зависят от характера текстов и целого ряда иных их особенностей.
| Таблица 1. Частота появления букв Буква | Частота | Буква | Частота | Буква | Частота | Буква | Частота |
| пробел | 0,175 | o | 0,090 | е, ë | 0,072 | а | 0,062 |
| и | 0,062 | т | 0,053 | н | 0,053 | с | 0,045 |
| р | 0,040 | в | 0,038 | л | 0,035 | к | 0,028 |
| м | 0,026 | д | 0,025 | п | 0,023 | у | 0,021 |
| я | 0,018 | ы | 0,016 | з | 0,016 | ъ, ь | 0,014 |
| б | 0,014 | г | 0,013 | ч | 0,012 | й | 0,010 |
| х | 0,009 | ж | 0,007 | ю | 0,006 | ш | 0,006 |
| ц | 0,004 | щ | 0,003 | э | 0,003 | ф | 0,00 |
По этим причинам в дальнейшем мы ограничим себя рассмотрением только шенноновских сообщений, т.е. будем учитывать различную (априорную) вероятность появления знаков в тексте, но не их корреляции.
Со следующего шага мы начнем рассматривать теорию кодирования.
Дата добавления: 2015-07-22; просмотров: 1660;
