СВЯЗЬ МЕЖДУ ЭНТРОПИЕЙ И ИНФОРМАЦИЕЙ

Рассмотрим пример.

В ящике имеются 2 белых шара и 4 черных.

Из ящика извлекают последовательно два шара без возврата.

Найти энтропию, связанную с первым и вторым извлечениями, а также энтропию обоих извлечений.

Будем считать опытом извлечение первого шара.

Он имеет два исхода:

· A1 – вынут белый шар; его вероятность p(A1) = 2/6 = 1/3;

· A2 – вынут черный шар; его вероятность p(A2)=1 – p(A1) = 2/3.

Эти данные позволяют с помощью (1.4) сразу найти H( ):

H( )= – p(A₁)log2 p(A₁) – p(A₂)log2 p(A₂) = –1/3 log₂1/3 – 2/3 log₂2/3 = 0,918 бит

Опыт – извлечение второго шара также имеет два исхода:

· B₁ – вынут белый шар;

· B₂ – вынут черный шар,

Однако их вероятности будут зависеть от того, каким был исход опыта .

В частности:

Следовательно, энтропия, связанная со вторым опытом, является условной и, согласно (1.8) и (1.9), равна:

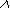
Наконец, из (1.10): H( ) = 0,918 + 0,888 = 1,806 бит.

Из рассмотренного примера видно как предшествующий опыт ( ) может уменьшить количество исходов и, следовательно, неопределенность последующего опыта ( ).

Разность H( ) и 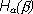, очевидно, показывает, какие новые сведения относительно мы получаем, произведя опыт . Эта величина называется информацией относительно опыта , содержащейся в опыте .

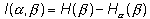(1.13)

Данное выражение открывает возможность численного измерения количества информации, поскольку оценивать энтропию мы уже умеем.

Из него легко получить ряд следствий.

Следствие 1. Поскольку единицей измерения энтропии является бит, то в этих же единицах может быть измерено количество информации.

Следствие 2. Пусть опыт = , т.е. просто произведен опыт . Поскольку он несет полную информацию о себе самом, неопределенность его исхода полностью снимается, т.е. =0.

Тогда I( , ) = H ( ), т.е. можно считать, что энтропия равна информации относительно опыта, которая содержится в нем самом.

Можно построить уточнение: энтропия опыта равна той информации, которую мы получаем в результате его осуществления.

Отметим ряд свойств информации.

I( , ) 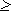0, причем I( , ) = 0 тогда и только тогда, когда опыты и независимы. Это свойство непосредственно вытекает из (1.10) и (1.13).

I( , ) = I( , ), т.е. информация симметрична относительно последовательности опытов.

Следствие 2 и представление энтропии в виде (1.4) позволяют записать:

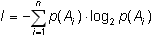(1.14)

т.е. информация опыта равна среднему значению количества информации, содержащейся в каком-либо одном его исходе.

Рассмотрим ряд примеров применения формулы (1.14).

Пример 1. Какое количество информации требуется, чтобы узнать исход броска монеты? В данном случае n=2 и события равновероятны, т.е. p1=p2=0,5. Согласно (1.14):

I = – 0,5•log₂0,5 – 0,5•log₂0,5 = 1 бит

Пример 2. Игра "Угадайка – 4". Некто задумал целое число в интервале от 0 до 3. Наш опыт состоит в угадывании этого числа. На наши вопросы Некто может отвечать лишь "Да" или "Нет". Какое количество информации мы должны получить, чтобы узнать задуманное число, т.е. полностью снять начальную неопределенность? Как правильно построить процесс угадывания?

Исходами в данном случае являются: A1 – "задуман 0", A2 – "задумана 1", A3 – "задумана 2", A4 – "задумана 3".

Конечно, предполагается, что вероятности быть задуманными у всех чисел одинаковы. Поскольку n = 4, следовательно, p(Ai)=1/4, log2 p(Ai) = –2 и I = 2 бит. Таким образом, для полного снятия неопределенности опыта (угадывания задуманного числа) нам необходимо 2 бита информации.

Теперь выясним, какие вопросы необходимо задать, чтобы процесс угадывания был оптимальным, т.е. содержал минимальное их число.

Здесь удобно воспользоваться так называемым выборочным каскадом:

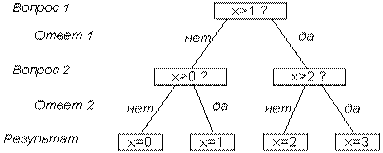
Таким образом, для решения задачи оказалось достаточно 2-х вопросов независимо от того, какое число было задумано. Совпадение между количеством информации и числом вопросов с бинарными ответами неслучайно.

Количество информации численно равно числу вопросов с равновероятными бинарными вариантами ответов, которые необходимо задать, чтобы полностью снять неопределенность задачи.

В рассмотренном примере два полученных ответа в выборочном каскаде полностью сняли начальную неопределенность.

Подобная процедура позволяет определить количество информации в любой задаче, интерпретация которой может быть сведена к парному выбору.

В такой процедуре все n исходов равновероятны. В этом случае для формулы (1.14) все

I = log₂n (1.15)

Эта формула была выведена в 1928 г. американским инженером Р.Хартли и носит его имя. Она связывает количество равновероятных состояний (n) и количество информации в сообщении (I), о том, что любое из этих состояний реализовалось.

Смысл этой формулы в том, что, если некоторое множество содержит n элементов и x принадлежит данному множеству, то для его выделения (однозначной идентификации) среди прочих требуется количество информации, равное log₂n.

Частным случаем применения формулы (1.15) является ситуация, когда n=2^k; подставляя это значение в (1.15), очевидно, получим:

I = k бит (1.16)

Таким образом, величина k равна количеству вопросов с бинарными равновероятными ответами, которые определяли количество информации в задачах, решаемых методом парного выбора

Пример 3. Случайным образом вынимается карта из колоды в 32 карты. Какое количество информации требуется, чтобы угадать, что это за карта? Как построить угадывание?

Для данной задачи n = 2⁵, значит, k = 5 и, следовательно, I = 5 бит. Последовательность вопросов придумайте самостоятельно.

Выражение (1.13) интерпретировать следующим образом: если начальная энтропия опыта H₁, а в результате сообщения информации I энтропия становится равной H₂ (очевидно, H₁ 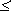H₂), то

I = H₁ – H₂,

т.е. информация равна убыли энтропии.

В частном случае, если изначально равновероятных исходов было n₁, а в результате передачи информации I неопределенность уменьшилась, и число исходов стало n₂ (очевидно, n₂ 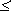n₁), то из (1.15) легко получить:

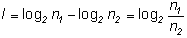
Таким образом, можно дать следующее определение:

Информация – это содержание сообщения, понижающего неопределенность некоторого опыта с неоднозначным исходом. Убыль связанной с ним энтропии является количественной мерой информации.

В случае равновероятных исходов информация равна логарифму отношения числа возможных исходов до и после (получения сообщения).