Свойства энтропии

1. Как следует из (1.4), H = 0 только в двух случаях:

· Какая-либо из вероятностей p(A_j) = 1;

Однако, при этом следует, что все остальные p(Ai) = 0 (i 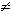j), т.е. реализуется ситуация, когда один из исходов является достоверным (и общий итог опыта перестает быть случайным);

· Все вероятности p(Ai) = 0,

То есть никакие из рассматриваемых исходов опыта невозможны, поскольку нетрудно показать, что

Во всех остальных случаях, очевидно, что H > 0.

2. Очевидным следствием свойства аддитивности (1.1) будет утверждение, что для двух независимых опытов и

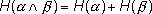(1.5)

Энтропия сложного опыта, состоящего из нескольких независимых, равна сумме энтропий отдельных опытов.

3. Пусть имеется два опыта с одинаковым числом исходов n, но в одном случае они равновероятны, а в другом – нет. Каково соотношение энтропий опытов?

Примем без доказательства следующее утверждение:

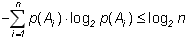(1.7)

То есть при прочих равных условиях наибольшую энтропию имеет опыт с равновероятными исходами. Другими словами, энтропия максимальна в опытах, где все исходы равновероятны.