Понятие условной энтропии

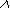
Найдем энтропию сложного опыта в том случае, если опыты не являются независимыми, т.е. если на исход оказывает влияние результат опыта .

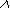
Например, если в ящике всего два разноцветных шара и состоит в извлечении первого, а – второго из них, то полностью снимает неопределенность сложного опыта , т.е. оказывается

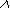
H( ) = H( ),

а не сумме энтропии, как следует из (1.5).

Связь между на 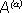могут оказывать влияние на исходы из 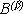, т.е. некоторые пары событий Ai 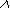Bj не являются независимыми.

Доказано, что для энтропии сложного опыта справедливо соотношение:

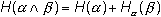,(1.10)

где 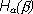есть средняя условная энтропия опыта при условии выполнении опыта .

Полученное выражение представляет собой общее правило нахождения энтропии сложного опыта. При этом выражение (1.5) является частным случаем (1.10) при условии независимости опытов и .

Относительно условной энтропии можно высказать следующие утверждения:

1. Условная энтропия является величиной неотрицательной.

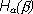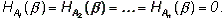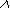
= 0 только в том случае, если любой исход полностью определяет исход (как в примере с двумя шарами), т.е. В этом случае H ( ) = H ( ).

2. Если опыты и независимы, то 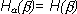, причем это оказывается наибольшим значением условной энтропии. Другими словами, опыт не может повысить неопределенность опыта ; он может либо не оказать никакого влияния (если опыты независимы), либо понизить энтропию .

Приведенные утверждения можно объединить одним неравенством:

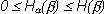(1.11)

т.е. условная энтропия не превосходит безусловную.

Из соотношений (1.10) и (1.11) следует, что

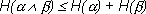(1.12)

причем равенство реализуется только в том случае, если опыты и независимы.