X, y, z

А, Б, С.

Количественная характеристика опыта состоит в определении зна­чений некоторых величин, полученных в результате опыта.

Такие ве­личины, которые могут принимать в результате опыта различные зна­чения, причем до опыта невозможно предвидеть, какими именно они будут, называются случайными величинами.

Примерами случайных величин могут служить:

· ошибки и резуль­таты измерений,

· время безотказной работы прибора или системы

· рост и вес наугад выбранного человека,

· координаты точки попадания (разрыва снаряда) при выстреле,

· число попаданий при п выстрелах.

Будем обозначать случайные величины прописными буквами, преимущественно из конца латинского алфавита, а их конкретные значения — соответствующими малыми буквами. Например, случай­ные величины будем обозначать

X, У, Z,

а их конкретные значения, получаемые в результате опыта, — соответственно

x, y, z

Эти зна­чения называются возможными значениями или реализациями слу­чайных величин

X, У, Z.

С каждой случайной величиной можно связать различные собы­тия.

Типичным событием, связанным со случайной величиной, явля­ется событие, состоящее в том, что эта случайная величина примет в результате опыта какое-нибудь значение, принадлежащее данному множеству, безразлично какое именно.

Такое событие коротко назы­вается попаданием случайной величины в данное множество.

1.5. Частота события.

Естественно сравнивать события по тому, как часто каждое из них появляется при повторении данного опыта.

Если при повторении опыта одно событие появляется чаще, чем другое, то говорят, что первое вероятнее второго.

Для сравнения событий необходимо предположить, что данный опыт можно производить сколько угодно раз.

Частотой события называется отношение числа его появлений к числу всех произведенных опытов.

Таким образом, если при п опытах событие А появилось т раз, то его частота в дайной серии опытов равна т/п.

1.6. Условные частоты.

В некоторых случаях частоту собы­тия приходится определять при дополнительном условии, что произо­шло некоторое другое событие.

Чтобы определить частоту события А при условии, что произошло событие В, необходимо учитывать не все произведенные опыты, а только те из них, в которых произошло со­бытие В.

Таким образом, если из п произведенных опытов событие В появи­лось в т опытах, причем в k: из этих т опытов появилось и событие А, то частота события Апри условии, что произошло событие В, равно k /т.

Эта частота, как правило, пе совпадает с частотой события А, вычисленной с учетом всех п произведенных опытов.

Частота события А, вычисленная с учетом только тех из произве­денных опытов, в которых появилось событие В, называется условной частотой события А относительно события В.

1.7. Свойства частот.

Событие называется невозможным и обозначается Æ, если оно не может произойти в результате данного опыта.

Событие называется достоверным и обозначается Ώ, если оно

обязательно происходит в результате данного опыта, т.е. не может не произойти.

События А₁, А₂ ,…, А_пназываются несовместными в данном опыте, если в результате этого опыта никакие два из пих пе могут появиться вместе.

Например,

· попадание и промах при одном выстреле,

· выпаде­ние 1 очка, 2 очков и 3 очков нри одном бросании игральной кости.

Два события, несовместные в одном опыте, могут оказаться сов­местными в другом опыте. Например, попадание и промах несовмест­ны при одном выстреле.

Однако они совместны, если за один опыт считаются два выстрела.

Ос­новные свойства частот событий.

1. Частота любого события представляет собой неотрицательное число, не превосходящее 1, причем частота невозможного события равна 0, а частота достоверного события равна 1.

2. Частота появления одного из несовместных событий, безразлич­но какого именно, равна сумме их частот.

Это следует непосредствен­но из того, что число появлений сложного события, представляющего собой появление какого-нибудь из несовместных событий, равно сум­ме чисел появлений этих событий.

3. Частота совместного появления двух событий А и В равна ча­стоте одного из них, умноженной на условную частоту другого.

Для доказательства достаточно заметить, что если при п опытах А появи­лось т раз, а В – k раз, причем l раз вместе с А, а к – l раз без А, то частота совместного появления А и В равна l /п, частота А рав­на m/n, а условная частота В относительно А равна l/т.

Очевидно, что если частота события в данной серии опытов рав­на 0 (или 1), то из этого не следует, что событие невозможно (до­стоверно).

Так, например, если при пяти бросаниях монеты герб не появился ни разу, то из этого не следует, что появление герба невоз­можно.

1.8. Вероятность события.

Экспериментально установлено:

· При малом числе опытов частота события принимает со­вершенно случайно различные значения,

· При неограниченном уве­личении числа опытов она проявляет тенденцию стабилизироваться около некоторого характерного для данного события значения.

Допустим, что некоторый опыт неограниченно повторяется и после каждого опыта вычисляется частота события с учетом всех уже произведенных опытов.

При этом обнаруживается, что вначале, когда число произведенных опытов мало, случайный результат каждого опыта существенно изменяет частоту события.

Однако но мере возрас­тания числа опытов влияние результата каждого нового опыта умень­шается.

Так, например, результат тысячного опыта изменяет частоту меньше, чем на 0,001.

Частота как бы стремится перестать быть слу­чайной и стабилизируется около некоторого значения.

Устойчивость частот событий дает основание считать, что с каж­дым событием связано некоторое число — вероятность этого собы­тия, — около которого стремится стабилизироваться его частота.

Так, например, частота появления герба при бросании монеты, очевидно, должна стабилизироваться около 1/2. Следовательно, вероятность по­явления герба равна 1 /2.

Вероятность события А обозначается Р{А). Это, конечно, не ис­ключает применения сокращенных обозначений, например Р{А) = р и т.п.

Понятие вероятности события является первичным в теории ве­роятностей и поэтому не нуждается в определении.

Вероятность события в данном опыте — его объективная харак­теристика. Она имеет вполне определенное значение независимо от того, собираемся мы производить опыты или нет.

1.9. Выборочное среднее.

Совокупность значений наблюдаемых величин, полученных в ре­зультате опытов, называется выборкой.

Получив выборку, необходимо прежде всего определить положе­ние значений случайной величины на числовой прямой и их рассеи­вание, т.е. размеры занимаемой ими области.

За характеристику положения экспериментальных точек обычно принимают среднее арифметическое значение случайной величины, называемое выборочным средним.

Предположим, что случайная ве­личина X приняла в результате п опытов значения х₁, … , х_{n .}

Тогда выборочное среднее определяется формулой

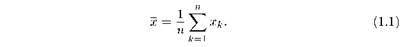
Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех ее значений на соответствующие им вероятности:

_n

М(Х)=∑ x_iр_{i =} x₁р₁ + x₂р₂+…+ x_nр_n

i=1

1.10. Выборочные дисперсия и среднее квадратическое отклонение.

За экспериментальную характеристику рассеивания значений скалярной случайной величины обычно принимают среднее арифметическое значение квадратов отклонений экспериментальных значений случайной величины от выборочного среднего.

Эта харак­теристика называется выборочной дисперсией случайной величины.

Если в результате п опытов случайная величина X приняла зна­чения х₁, … , х_{n ,} то ее выборочная дисперсия определяется формулой

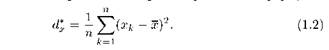
Или же используя понятие вероятности

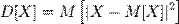
Получится, что дисперсия - это средний квадрат отклонений от среднего значения.

(Математическое ожидание квадрата отклонения случайной величины от математического ожидания этой случайной величины).

То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности.

Разница между отдельным значением и средней отражает меру отклонения.

В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании.

Затем, имея квадраты отклонений, мы просто рассчитываем среднюю арифметическую величину квадрата отклонений.

Однако в чистом виде дисперсия не используется.

Это вспомогательный и промежуточный показатель, который используется для других видов статистического анализа.

Недостатком выборочной дисперсии с практической точки зре­ния является отсутствие наглядности — она имеет размерность квад­рата случайной величины.

Поэтому за практическую характери­стику рассеивания значений случайной величины обычно принима­ют выборочное среднее квадратическое отклонение, представляющее собой положительный квадратный корень из выборочной диспер­сии, σ* =Öd_x^*

2. ЭНТРОПИЯ КАК МЕРА НЕОПРЕДЕЛЕННОСТИ