Решение. Пример 8.Найти частную производную и полную производную , если , где .
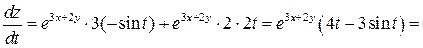
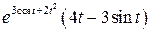 .
.
Пример 8.Найти частную производную 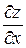 и полную производную
и полную производную 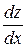 , если
, если 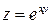 , где
, где 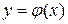 .
.
2. Случай нескольких независимых переменных.Если 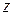 сложная функция нескольких независимых переменных, например
сложная функция нескольких независимых переменных, например 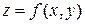 , где
, где 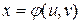 ;
; 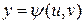 (
( 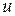 и
и 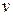 – независимые переменные;
– независимые переменные; 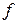 ,
, 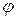 и
и 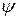 – дифференцируемые функции), то частные производные
– дифференцируемые функции), то частные производные 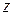 по
по 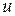 и
и 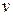 выражаются так:
выражаются так:
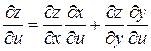 ;
; 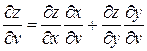 .
.
Во всех рассмотренных случаях справедлива формула
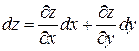
(свойство инвариантности первого дифференциала).
Пример 9.Найти 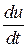 , если
, если 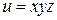 , где
, где 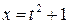 ,
, 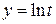 ,
, 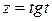 .
.
Пример 10.Показать, что функция 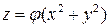 удовлетворяет уравнению
удовлетворяет уравнению 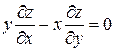 .
.
Решение.Обозначим 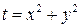 . Тогда
. Тогда
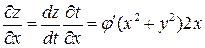 ,
, 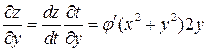 .
.
Подставив частные производные в левую часть уравнения, будем иметь
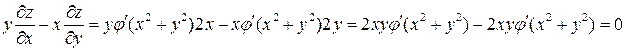 Пример 11.Найти
Пример 11.Найти 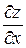 и
и 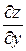 , если
, если 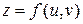 , где
, где 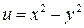 ,
, 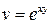 .
.
Дата добавления: 2015-08-11; просмотров: 606;
