Дифференциал функции нескольких переменных.

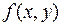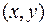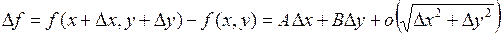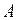Определение. Если приращение функции в точке можно записать в виде , где и 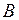зависят только от 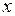и 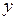, и не зависят от 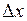, , 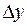то функция называется дифференцируемой в точке .

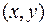Выражение 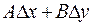называется дифференциалом функции 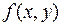в точке 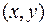и обозначается символом .

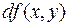Теорема. Если функция 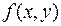дифференцируема в точке 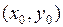, то она имеет в этой точке частные производные, причем .

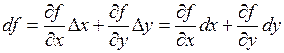Дифференциал функции 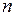переменных записывается аналогично:

.

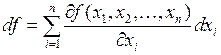Теорема (достаточное условие дифференцируемости) Если функция 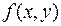имеет в точке 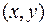непрерывные частные производные, то она дифференцируема в этой точке.

Утверждение.Функция 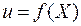, дифференцируемая в точке 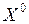, является непрерывной в этой точке.