Дифференцирование сложной функции.
1. Случай одной независимой переменной. Если 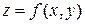 дифференцируемая функция аргументов
дифференцируемая функция аргументов 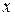 и
и 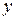 , которые в свою очередь являются дифференцируемыми функциями независимой переменной
, которые в свою очередь являются дифференцируемыми функциями независимой переменной 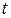 :
: 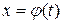 ;
; 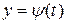 , то производная сложной функции
, то производная сложной функции 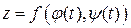 может быть вычислена по формуле
может быть вычислена по формуле
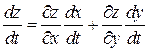 , (*)
, (*)
которая называется формулой полной производной.
В частности, если 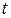 совпадает с одним из аргументов, например
совпадает с одним из аргументов, например 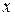 , то «полная» производная
, то «полная» производная 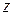 по
по 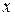 будет
будет
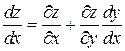
Пример 7.Найти 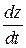 , если
, если 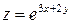 , где
, где 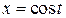 ,
, 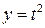 .
.
Дата добавления: 2015-08-11; просмотров: 525;
