Дифференциальное исчисление функции нескольких переменных.

Определение 1.Пусть у функции 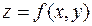переменная 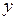зафиксирована, а переменная 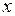получает приращение 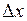. Тогда приращение функции будет .

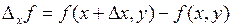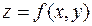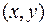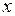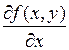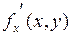Если существует предел , то его называют частной производной от функции в точке по переменной и обозначают: или , или .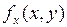

Аналогично определяется частная производная по переменной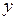

При нахождении частной производной применимы все формулы и правила дифференцирования функции одной переменной, так как по определению мы фиксируем все переменные, кроме одной, и фактически имеем дело с функцией одной переменой. Если, например, находим производную по 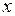, то все остальные аргументы рассматриваем как константы.

Пример 5.Найти частные производные функции .

Решение. При нахождении 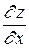считаем, что 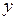– константа, а 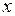– переменная величина, поэтому 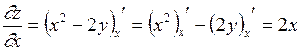. Аналогично, .

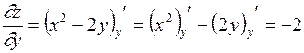Пример 6.Найти частные производные функции

.

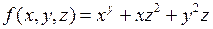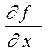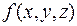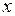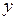Решение. Находим , считая, что – функция одного аргумента – , а и 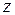– константы: .

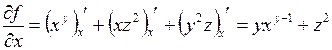Замечание. Для функции многих переменных из существования конечных частных производных в точке 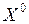не следует непрерывность функции в этой точке.