Свойства непрерывных функций нескольких переменных.
Свойство 1.Если 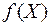 и
и 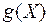 заданы на одном и том же множестве
заданы на одном и том же множестве 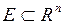 , и непрерывны в некоторой точке
, и непрерывны в некоторой точке 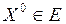 , то функции
, то функции 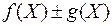 ,
, 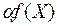 ,
, 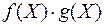 , а при условии, что
, а при условии, что 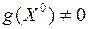 и
и 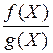 – непрерывны в точке
– непрерывны в точке 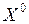 .
.
Свойство 2.Если функция 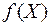 непрерывна на замкнутом ограниченном множестве
непрерывна на замкнутом ограниченном множестве 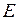 , то:
, то:
1) она ограничена на этом множестве;
2) она достигает на этом множестве своих наибольшего 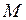 и наименьшего
и наименьшего 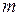 значений;
значений;
3) для любого числа 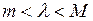 найдется такая точка
найдется такая точка 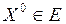 , что
, что 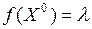 .
.
Дата добавления: 2015-08-11; просмотров: 631;
