Непрерывность функции переменных.
Определение 7.Функцию 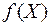 , определенную в окрестности точки
, определенную в окрестности точки 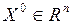 (и в самой точке), называют непрерывной в точке
(и в самой точке), называют непрерывной в точке 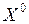 , если
, если 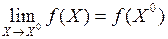 .
.
Точки пространства 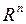 , в которых функция
, в которых функция 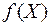 не обладает свойством непрерывности называются точками разрыва функции.
не обладает свойством непрерывности называются точками разрыва функции.
Точку 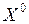 называют точкой разрыва в случае:
называют точкой разрыва в случае:
1) 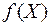 определена во всех точках некоторой окрестности точки
определена во всех точках некоторой окрестности точки 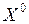 , кроме самой точки
, кроме самой точки 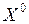 ;
;
2) функция 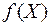 определена во всех точках окрестности
определена во всех точках окрестности 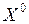 и в самой точке
и в самой точке 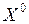 , но не существует предела
, но не существует предела 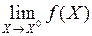
3) функция 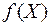 определена во всех точках окрестности
определена во всех точках окрестности 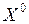 и в самой точке
и в самой точке 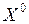 , и существует предел
, и существует предел 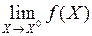 , но
, но 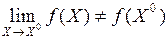 .
.
Определение 8.Функция, непрерывная в каждой точке множества 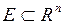 называется непрерывной на множестве
называется непрерывной на множестве 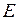 .
.
Дата добавления: 2015-08-11; просмотров: 545;
