Решение. Отнесем треугольник к вспомогательной системе координат x0, y0

Отнесем треугольник к вспомогательной системе координат x⁰, y⁰. В качестве элементарной площади возьмем полоску на расстоянии y⁰ толщиной dy⁰ и переменной ширины b(y⁰) так, что

.

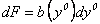Из подобия треугольников нетрудно установить, что:

,

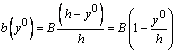тогда .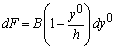

Статический момент 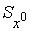будет равен

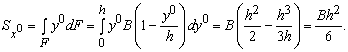
По аналогии получим

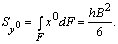
Площадь треугольника

.

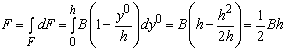Координаты центра тяжести C определим по формулам:

Через точку C проводим центральные оси x, y параллельные осям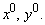

Момент инерции 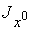и аналогично 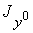равны:

,

.

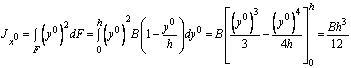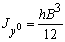Для определения момента инерции относительно центральной оси x воспользуемся формулой при параллельном переносе осей

.

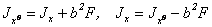Так как , то

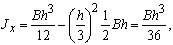
Центробежный момент

,

где ; .

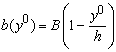Интегрируя, получаем

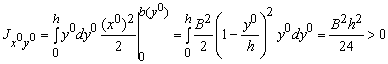
Перейдя к центральным осям x и y, получим

.

Определение направлений главных осей:

.

Проводим главные центральные оси 1 и 2.

Если, например, 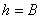, то имеем равнобедренный треугольник, для которого , , 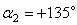. Тогда:

.

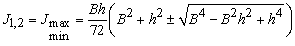Пример 4.

Определить площадь и моменты инерции относительно главных центральных осей инерции круглого поперечного сечения диаметра 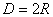(см. рис.).