Ускорение материальной точки
При движении материальной точки ее скорость 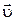 может изменяться со временем. Для характеристики изменения скорости вводят ускорение как производную по времени вектора скорости:
может изменяться со временем. Для характеристики изменения скорости вводят ускорение как производную по времени вектора скорости:
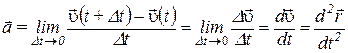 (1.14)
(1.14)
или в проекциях на декартовы оси координат
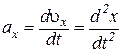 ,
,  ,
,  . (1.15)
. (1.15)
Ускорение 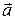 , в отличие от скорости
, в отличие от скорости 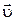 , может иметь любую ориентацию по отношению к направлению движения материальной точки. Очевидно, что модуль ускорения связан с его проекциями соотношением
, может иметь любую ориентацию по отношению к направлению движения материальной точки. Очевидно, что модуль ускорения связан с его проекциями соотношением
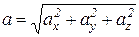 . (1.16)
. (1.16)
По аналогии с п.1.3.3 вводят средний вектор ускорения 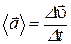 , его модуль
, его модуль 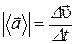 и среднее ускорение
и среднее ускорение 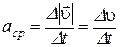 .
.
В общем случае, когда изменяется как модуль скорости 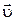 , так и ее направление (случай неравномерного криволинейного движения), движение характеризуют с помощью естественных составляющих вектора
, так и ее направление (случай неравномерного криволинейного движения), движение характеризуют с помощью естественных составляющих вектора 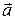 , который называется полным ускорением.
, который называется полным ускорением.
Представим вектор скорости в естественном виде:
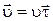 , (1.17)
, (1.17)
где 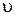 – модуль скорости, а
– модуль скорости, а 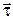 – орт скорости.
– орт скорости.
Используя определение (1.14), получим
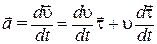 . (1.18)
. (1.18)
Первую составляющую 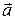 в правой части равенства (1.18) обозначим
в правой части равенства (1.18) обозначим
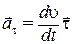 , (1.19)
, (1.19)
а вторую
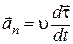 . (1.20)
. (1.20)
Смысл составляющей 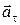 достаточно очевиден: она характеризует быстроту изменения со временем модуля скорости. Модуль этой составляющей равен
достаточно очевиден: она характеризует быстроту изменения со временем модуля скорости. Модуль этой составляющей равен 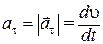 , а направлена она по касательной к траектории в направлении движения
, а направлена она по касательной к траектории в направлении движения 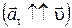 , если скорость по модулю возрастает
, если скорость по модулю возрастает 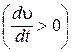 , и в противоположном движению направлении
, и в противоположном движению направлении 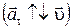 , если скорость по модулю убывает
, если скорость по модулю убывает 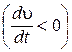 . Поэтому эта естественная составляющая ускорения называется тангенциальным (касательным) ускорением.
. Поэтому эта естественная составляющая ускорения называется тангенциальным (касательным) ускорением.
Вторая составляющая 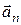 характеризует быстроту изменения вектора скорости по направлению (см. (1.13) из п. 1.3.3 и ниже).
характеризует быстроту изменения вектора скорости по направлению (см. (1.13) из п. 1.3.3 и ниже).
Для выяснения величины и направления составляющей 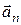 рассмотрим для простоты плоское криволинейное движение (рис 1.4). Будем считать, что точки 1 и 2, соответствующие моментам времени t и t+Dt, лежат на траектории достаточно близко друг к другу. В этом случае длину дуги траектории DS между токами 1 и 2 можно считать приближенно дугой окружности радиуса R. Перене-
рассмотрим для простоты плоское криволинейное движение (рис 1.4). Будем считать, что точки 1 и 2, соответствующие моментам времени t и t+Dt, лежат на траектории достаточно близко друг к другу. В этом случае длину дуги траектории DS между токами 1 и 2 можно считать приближенно дугой окружности радиуса R. Перене-
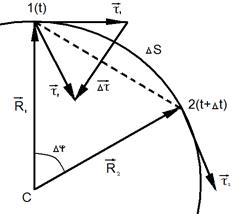 Рис. 1.4
Рис. 1.4
| сем параллельно орт 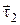 в точку 1. Из рис. 1.4 видно, что треугольник 12С и треугольник, образованный ортами в точку 1. Из рис. 1.4 видно, что треугольник 12С и треугольник, образованный ортами 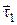 , , 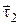 и приращением и приращением 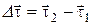 , подобны. Следовательно, , подобны. Следовательно,
 .
Поэтому с учетом .
Поэтому с учетом 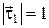 получим получим
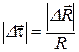 .
Величину составляющей .
Величину составляющей 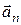 найдем из (1.20) с помощью ряда равенств найдем из (1.20) с помощью ряда равенств
|
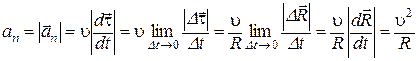 ,
,
то есть
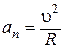 . (1.21)
. (1.21)
Легко видеть, что при Dt 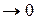 вектор
вектор 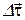 , а значит и
, а значит и 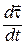 , направлены перпендикулярно касательной к траектории
, направлены перпендикулярно касательной к траектории 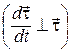 к центру дуги DS окружности. Введя единичный вектор нормали
к центру дуги DS окружности. Введя единичный вектор нормали 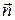
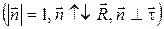 , выражению (1.21) можно придать вид
, выражению (1.21) можно придать вид
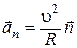 . (1.22)
. (1.22)
В случае произвольной криволинейной траектории R означает радиус кривизны траектории в данной ее точке:
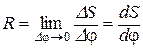 . (1.23)
. (1.23)
Из-за своего направления составляющая 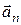 называется нормальным (центростремительным) ускорением.
называется нормальным (центростремительным) ускорением.
Теперь соотношению (1.18) можно придать вид (рис 1.5)
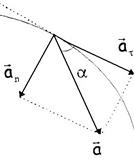 Рис.1.5
Рис.1.5
| 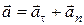 , (1.24)
а так как , (1.24)
а так как 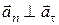 , то , то
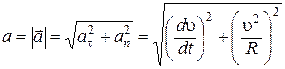 и и 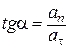 (1.25)
Соотношения (1.25) определяют величину и направление полного ускорения (1.25)
Соотношения (1.25) определяют величину и направление полного ускорения 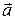 .
В качестве примера рассмотрим один из результатов, вытекающих из соотношений (1.19), (1.22) и (1.24). .
В качестве примера рассмотрим один из результатов, вытекающих из соотношений (1.19), (1.22) и (1.24).
|
Пусть тангенциальное ускорение равно нулю 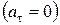 , а модуль нормального ускорения постоянен
, а модуль нормального ускорения постоянен 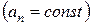 . Условие
. Условие 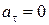 означает, что
означает, что 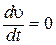 , то есть модуль скорости
, то есть модуль скорости 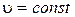 . Поэтому движение равномерное.
. Поэтому движение равномерное.
Теперь из условия 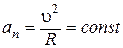 следует, что радиус кривизны траектории R тоже постоянен, что для плоской кривой означает, что траектория есть окружность (в общем случае – винтовая линия).
следует, что радиус кривизны траектории R тоже постоянен, что для плоской кривой означает, что траектория есть окружность (в общем случае – винтовая линия).
Выводы: Ускорение характеризует быстроту изменения вектора скорости и равно производной скорости по времени. При криволинейном движении вектор ускорения имеет две составляющие: тангенциальное и нормальное ускорение. Тангенциальное ускорение характеризует скорость изменения модуля скорости и направлено по касательной к траектории движения. Нормальное ускорение характеризует скорость изменения вектора скорости по направлению и направлено по нормали к касательной к центру кривизны траектории точки.
Контрольные вопросы
1.7. Опишите движения материальной точки, исходя из условий а) at=0, an=0; б) at=const, an=0; в) at=аt(t), an=0; г) at=0, an=const.
1.8. Возможно ли движение при условии 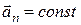 ?
?
Дата добавления: 2015-08-08; просмотров: 2151;
