Скорость материальной точки
Поскольку при движении материальной точки изменяется ее положение относительно выбранной системы отсчета, то возникает важный вопрос: Как быстро это положение изменяется? Физической величиной, с помощью которой отвечают на этот вопрос, является скорость.
Скоростью материальной точки 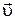 называется вектор, равный производной радиус-вектора
называется вектор, равный производной радиус-вектора 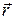 по времени:
по времени:
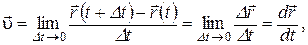 (1.5)
(1.5)
или в проекциях на декартовы координатные оси
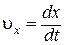 ,
, 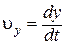 ,
, 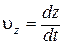 , (1.6)
, (1.6)
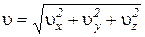 .
.
Так как хорда 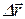 (рис 1.2), стягивающая дугу траектории l12, в пределе при
(рис 1.2), стягивающая дугу траектории l12, в пределе при 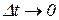
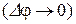 совпадает с касательной, то вектор скорости направлен по касательной к траектории в сторону движения материальной точки.
совпадает с касательной, то вектор скорости направлен по касательной к траектории в сторону движения материальной точки.
В частности, если модуль скорости 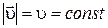 , то такое движение называется равномерным.
, то такое движение называется равномерным.
Если детальная характеристика движения за промежуток времени 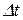 несущественна, то используют средние величины:
несущественна, то используют средние величины:
– средний вектор скорости
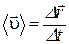 , (1.7)
, (1.7)
– модуль скорости
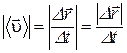 , (1.8)
, (1.8)
– средняя скорость
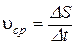 , (1.9)
, (1.9)
где DS – путь, пройденный материальной точкой за время Dt. Обратите внимание на то, что  – скалярная величина. В общем случае произвольного движения материальной точки
– скалярная величина. В общем случае произвольного движения материальной точки 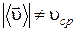 .
.
Часто полезно бывает знать, с какой скоростью изменяется со временем
расстояние между материальной точкой и началом координат (как быстро изменяется модуль радиус-вектора 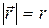 ), и с какой скоростью изменяется направление радиус-вектора относительно осей координат системы отсчета? Ответить на эти вопросы проще всего, если воспользоваться естественной формой представления радиус-вектора
), и с какой скоростью изменяется направление радиус-вектора относительно осей координат системы отсчета? Ответить на эти вопросы проще всего, если воспользоваться естественной формой представления радиус-вектора
 , (1.10)
, (1.10)
которая учитывает тот факт, что у любого вектора есть две естественные характеристики: величина и направление. Здесь 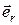 – орт вектора
– орт вектора 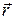 , то есть вектор, модуль которого равен единице
, то есть вектор, модуль которого равен единице 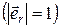 , а направление совпадает с направлением радиус-вектора
, а направление совпадает с направлением радиус-вектора 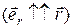 .
.
Используя (1.5) и (1.10), получим
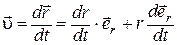 . (1.11)
. (1.11)
В соотношении (1.11) вектор 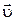 представлен в виде двух составляющих, первая из которых
представлен в виде двух составляющих, первая из которых
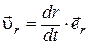 (1.12)
(1.12)
характеризует скорость изменения модуля радиус-вектора и направлена вдоль
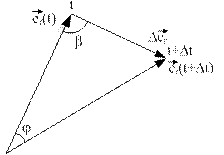 Рис.1.3 Рис.1.3
| 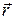 . Вторая составляющая . Вторая составляющая 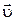
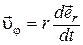 (1.13)
характеризует скорость изменения радиус-вектора по направлению и направлена перпендикулярно (1.13)
характеризует скорость изменения радиус-вектора по направлению и направлена перпендикулярно 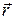 в сторону его поворота. Действительно, так как в сторону его поворота. Действительно, так как
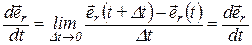 , , 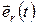 ,
то из рис. 1.3 следует, что при ,
то из рис. 1.3 следует, что при 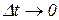 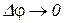
|
(угол поворота радиус-вектора 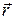 за время
за время 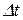 ). При этом
). При этом 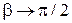 , значит при
, значит при 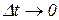
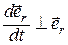 . Поэтому
. Поэтому 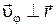 . Здесь надо учесть, что
. Здесь надо учесть, что 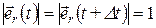 . Таким образом,
. Таким образом,
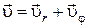 ;
; 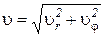 .
.
Выводы: Скорость материальной точки – есть производная радиус-вектора по времени, характеризует быстроту изменения радиус-вектора как по модулю, так и по направлению, направлена по касательной к траектории движения.
Контрольные вопросы
1.4. Покажите, что 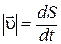 .
.
1.5. Может ли при прямолинейном движении выполняться условие 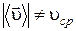 . При каком движении выполняется равенство между этими величинами?
. При каком движении выполняется равенство между этими величинами?
1.6. Что вы можете сказать о характере движения и виде траектории, если: а) 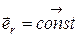 ; б)
; б) 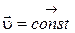 ; в)
; в) 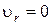 ,
, 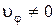 ; г)
; г) 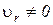 ,
, 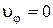 ; д)
; д) 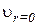 ,
, 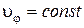 .
.
Дата добавления: 2015-08-08; просмотров: 1562;
