Кинематика твердого тела
Всякое сложное движение твердого тела можно представить как результат наложения друг на друга двух простых типов движения: поступательного и вращательного.
Поступательное движение – это движение, когда прямая, проведенная через любые две точки тела, остается параллельной самой себе (рис 1.10).
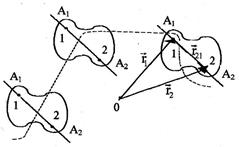 Рис 1.10
Рис 1.10
| Особенностью такого движения является то, что все точки твердого тела в любой момент времени имеют одинаковые скорости и ускорения. Поэтому при поступательном движении твердого тела достаточно описать движение только одной какой-либо точки тела.
Действительно, пусть в некоторый момент времени t положения двух произвольных точек тела 1 и 2 относительно точки отсчета О (рис 1.10) определяются радиус-векторами 
|
и  . Тогда взаимное их расположение в теле описывается вектором
. Тогда взаимное их расположение в теле описывается вектором  . При этом
. При этом
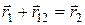 , (1.41)
, (1.41)
а так как тело твердое, то 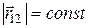 . При поступательном движении прямая, проходящая через точки 1 и 2, перемещается параллельно самой себе. Поэтому направление вектора
. При поступательном движении прямая, проходящая через точки 1 и 2, перемещается параллельно самой себе. Поэтому направление вектора 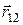 при движении тела не изменяется. Дифференцируя равенство (1.41) по времени с учетом постоянства
при движении тела не изменяется. Дифференцируя равенство (1.41) по времени с учетом постоянства 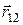 , получим
, получим
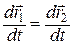 , или
, или 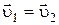 .
.
Дифференцируя последние равенства еще раз по времени, получим равенство ускорений:
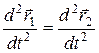 , или
, или 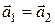 .
.
Поскольку точки 1 и 2 выбраны произвольно, то особенность поступательного движения доказана.
Вращательное движение – это движение, когда все точки твердого тела движутся по окружностям. При этом центры этих окружностей лежат на одной прямой, которая называется осью вращения (рис. 1.11). Ось вращения может пронизывать тело (рис. 1.11а) или находиться вне тела (рис. 1.11б).
Особенностью вращательного движения является то, что все точки тела в
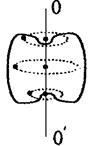
|
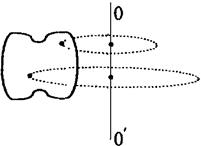
| любой момент времени t имеют относительно оси вращения одинаковые угловые скорости и угловые ускорения.
Описание вращательного движения с помощью угловых кинематических характеристик 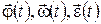 имеет громадное преимущество перед описанием с помощью линейных кинематических величин именно в силу указанной особенности вращательного движения. имеет громадное преимущество перед описанием с помощью линейных кинематических величин именно в силу указанной особенности вращательного движения.
|
| а) | б) | |
| Рис. 1.11 |
Если известно кинематическое уравнение вращательного движения 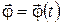 , то, зная радиус окружности, по которой вращается данная точка тела, с помощью (1.27), (1.30) и (1.32) можно легко определить ее линейные кинематические характеристики
, то, зная радиус окружности, по которой вращается данная точка тела, с помощью (1.27), (1.30) и (1.32) можно легко определить ее линейные кинематические характеристики 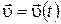 и
и 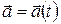 .
.
Теперь можно показать, что произвольное движение твердого тела представимо в виде наложения поступательного и вращательного движений.
Покажем это для случая плоского движения твердого тела.
Рассмотрим два произвольных положения тела при сложном его движении
 Рис. 1.12
Рис. 1.12
| (рис. 1.12).
Результирующее перемещение тела из положения  в в  можно осуществить бесконечным множеством способов. Например, поступательно переместить из положения можно осуществить бесконечным множеством способов. Например, поступательно переместить из положения 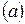 в в 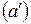 , а затем повернуть вокруг оси , а затем повернуть вокруг оси 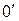 на угол на угол 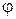 по часовой стрелке; или поступательно переместить из положения по часовой стрелке; или поступательно переместить из положения 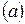 в положение в положение 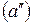 , и повернуть на тот же угол j относительно , и повернуть на тот же угол j относительно
|
оси 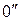 .Таким образом, элементарное перемещение
.Таким образом, элементарное перемещение 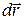 какой-либо точки твердого тела за время dt можно представить в виде суммы
какой-либо точки твердого тела за время dt можно представить в виде суммы
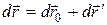 , (1.42)
, (1.42)
где 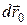 – одинаковое для всех точек тела перемещение при поступательном движении, а
– одинаковое для всех точек тела перемещение при поступательном движении, а 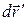 – перемещение при повороте на угол
– перемещение при повороте на угол 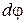 (может осуществляться относительно различных осей).
(может осуществляться относительно различных осей).
Из (1.42) следует, что
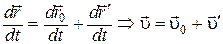 . (1.43)
. (1.43)
Здесь 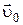 – скорость поступательного движения, одинаковая для всех точек тела, а
– скорость поступательного движения, одинаковая для всех точек тела, а 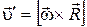 – линейная скорость точки при ее поворотах с угловой скоростью
– линейная скорость точки при ее поворотах с угловой скоростью  по окружности радиуса
по окружности радиуса 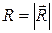 вокруг мгновенной оси. Отметим, что
вокруг мгновенной оси. Отметим, что
все точки тела имеют одинаковую угловую скорость 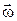 . Таким образом,
. Таким образом,
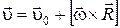 . (1.44)
. (1.44)
Выводы: Любое сложное движение твердого тела является результатом сложения поступательного и вращательного движений.
Контрольные вопросы
1.13. Можно ли произвольное перемещение твердого тела представить как результат а) только одних поворотов? б) только одного поступательного перемещения?
1.14. Может ли быть поступательным такое движение, при котором все точки твердого тела движутся по окружностям?
Ответы на контрольные вопросы
1.1.

| 
|
1.2. а) 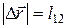 – движение прямолинейное,
– движение прямолинейное, 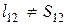 –на участке 1-2 направление движения изменяется; б)
–на участке 1-2 направление движения изменяется; б) 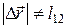 – движение криволинейное,
– движение криволинейное,  –на участке 1-2 направление движения не изменяется.
–на участке 1-2 направление движения не изменяется.
1.4. 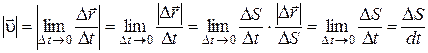 .
. 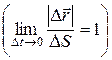 .
.
1.5. Может, если движение на прямолинейном участке траектории изменяет направление. Равенство 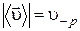 выполняется при неизменном направлении движения, когда
выполняется при неизменном направлении движения, когда 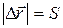 .
.
1.6. а) Условие 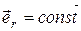 означает, что при движении (см. 1.10) может изменяться только модуль радиус-вектора. Поэтому движение прямолинейное на одной из ветвей прямой, проходящей через точку отсчета. Характер этого движения может быть любой, он определяется зависимостью модуля радиус-векто-ра от времени r=r(t); б) Условие
означает, что при движении (см. 1.10) может изменяться только модуль радиус-вектора. Поэтому движение прямолинейное на одной из ветвей прямой, проходящей через точку отсчета. Характер этого движения может быть любой, он определяется зависимостью модуля радиус-векто-ра от времени r=r(t); б) Условие  означает, что направление вектора
означает, что направление вектора 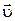 неизменно (движение прямолинейное) и модуль скорости постоянен (движение равномерное); в)
неизменно (движение прямолинейное) и модуль скорости постоянен (движение равномерное); в) 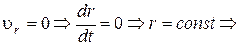 траектория лежит на поверхности сферы,
траектория лежит на поверхности сферы, 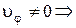 вид траектории, вообще говоря, произволен; г) Условие
вид траектории, вообще говоря, произволен; г) Условие 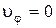 эквивалентно
эквивалентно 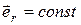 (см. случай а)); д) Условие
(см. случай а)); д) Условие 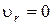 означает, что
означает, что 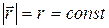 , а
, а 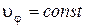 означает, что
означает, что 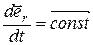 , следовательно, указанные условия определяют равномерное движение по окружности.
, следовательно, указанные условия определяют равномерное движение по окружности.
1.7. а) 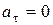 означает, что
означает, что 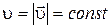 , а
, а 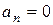 означает, что R=∞. Оба условия выполняются, если движение равномерное и прямолинейное; б) равнопеременное прямолинейное движение; в) прямолинейное движение, характер его определяется зависимостью
означает, что R=∞. Оба условия выполняются, если движение равномерное и прямолинейное; б) равнопеременное прямолинейное движение; в) прямолинейное движение, характер его определяется зависимостью 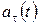 ; г) равномерное движение по винтовой линии.
; г) равномерное движение по винтовой линии.
1.8. Возможен только тривиальный случай 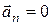 (прямолинейное движение).
(прямолинейное движение).
1.9. В этом случае 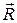 является радиусом кривизны траектории относительно мгновенной оси вращения: а) равномерное вращение; б) равнопеременное вращение вокруг мгновенной оси; в) равнопеременное вращение вокруг неподвижной оси; г) условие
является радиусом кривизны траектории относительно мгновенной оси вращения: а) равномерное вращение; б) равнопеременное вращение вокруг мгновенной оси; в) равнопеременное вращение вокруг неподвижной оси; г) условие 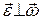 означает, что
означает, что 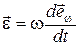 , а
, а 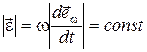 означает, что
означает, что 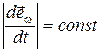 ,то есть материальная точка равномерно (
,то есть материальная точка равномерно ( 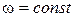 )вращается по окружности, плоскость которой, в свою очередь, равномерно поворачивается относительно неподвижного диаметра.
)вращается по окружности, плоскость которой, в свою очередь, равномерно поворачивается относительно неподвижного диаметра.
1.11. Если выбрать систему координат так, чтобы одна из ее плоскостей (например ХОУ) совпадала с плоскостью, в которой лежат постоянные векторы 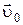 и
и 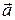 , то в этом случае
, то в этом случае 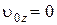 и
и 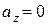 , поэтому из (1.38) сразу следует z=z0, что и означает движение в плоскости, параллельной ХОУ. Если при этом одну из осей (например, ОХ) направить вдоль
, поэтому из (1.38) сразу следует z=z0, что и означает движение в плоскости, параллельной ХОУ. Если при этом одну из осей (например, ОХ) направить вдоль 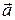 , то (1.38) примет вид
, то (1.38) примет вид
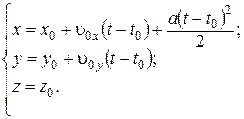
Исключая из первых двух соотношений время t, получим:
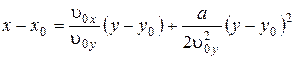 – уравнение параболы, лежащей в плоскости z=z0.
– уравнение параболы, лежащей в плоскости z=z0.
1.12. Уравнения (1.39), (1.40) получаются непосредственно из (1.37) и (1.38) с учетом (1.27), (1.30) и (1.33) для модулей векторов.
1.13. а) Можно, вокруг мгновенной оси вращения; б) Нельзя.
1.14. Может.
Дата добавления: 2015-08-08; просмотров: 1151;
