Кинематическими величинами

Из соотношения (1.27) непосредственно следует, что

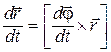
или с учетом (1.5) и (1.28)

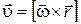. (1.30)

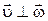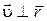Из (1.30) следует, что и , а величина скорости 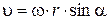. При движении точки вокруг неподвижной оси (рис 1.9, а) ( 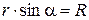, где R – радиус окружности), для модуля скорости имеем

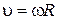(1.31)

Дифференцируя соотношение (1.30) по времени, получим

,

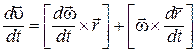или, используя (1.14), (1.29) и (1.5),

. (1.32)

Первое слагаемое представляет собой тангенциальную составляющую ускорения:

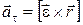, (1.33)

а второе слагаемое – нормальную составляющую ускорения

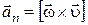. (1.34)

Чтобы убедиться в справедливости (1.33) и (1.34), рассмотрим вращение точки вокруг неподвижной оси. В этом случае

.

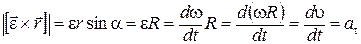Здесь использованы формулы (1.26), (1.29), (1.31), (1.19) и учтено, что R=const. Для (1.34) с учетом 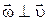и (1.31), (1.21) получим

.

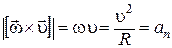Выводы: Вращательное движение материальной точки в равной мере может описываться как с помощью линейных кинематических величин 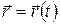, , 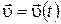, 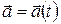так и с помощью угловых 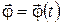, , 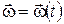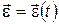. Между линейными и угловыми величинами существует взаимная связь, выражаемая соотношениями (1.27), (1.30) и (1.32-1.34).