Связь между линейными и угловыми величинами
 Найдем скорость
Найдем скорость  произвольной точки A твердого тела, вращающегося вокруг неподвижной оси OO’ с угловой скоростью
произвольной точки A твердого тела, вращающегося вокруг неподвижной оси OO’ с угловой скоростью  . Пусть положение точки A относительно некоторой точки O оси вращения характеризуется радиус-вектором
. Пусть положение точки A относительно некоторой точки O оси вращения характеризуется радиус-вектором  (рис.1.2.3). Воспользуемся формулой (1.2.1), поделив ее на соответствующий промежуток времени dt. Так как d
(рис.1.2.3). Воспользуемся формулой (1.2.1), поделив ее на соответствующий промежуток времени dt. Так как d  /dt =
/dt =  и d
и d  /dt =
/dt =  , то
, то
Рис.1.2.3.
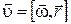 , (1.2.7)
, (1.2.7)
т. е. скорость у любой точки A твердого тела, вращающегося вокруг некоторой оси с угловой скоростью  , равна векторному произведению
, равна векторному произведению  на радиус-вектор
на радиус-вектор  точки A относительно произвольной точки O оси вращения (рис.1.2.3).
точки A относительно произвольной точки O оси вращения (рис.1.2.3).
Модуль вектора скорости υ = ωrsin 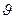 , или υ = ωρ,
, или υ = ωρ,
где ρ — радиус окружности, по которой движется точка A.
Продифференцировав (1.2. 7) по времени, найдем полное ускорение точки A: 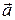 = [d
= [d  /dt,
/dt,  ] + [
] + [  ,d
,d  /dt], или
/dt], или
 (1.2.8)
(1.2.8)
В данном случае (ось вращения неподвижна) 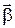 ||
||  , поэтому вектор [
, поэтому вектор [ 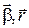 ] представляет собой тангенциальное ускорение
] представляет собой тангенциальное ускорение 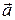 τ. Вектор же [
τ. Вектор же [  [
[ 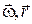 ]] — это нормальное ускорение
]] — это нормальное ускорение 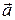 n. Проекции вектора
n. Проекции вектора 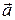 на орты τ и n равны:
на орты τ и n равны:
aτ = βz ρ, an = ω2 ρ.
Отсюда модуль полного ускорения 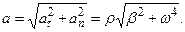
Дата добавления: 2015-08-08; просмотров: 826;
