Сложение угловых скоростей
 Рассмотрим движение твердого тела, вращающегося одновременно вокруг двух пересекающихся осей. Сообщим некоторому телу вращение с угловой скоростью
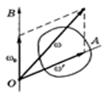
Рассмотрим движение твердого тела, вращающегося одновременно вокруг двух пересекающихся осей. Сообщим некоторому телу вращение с угловой скоростью  ’ вокруг оси ОА (рис.1.2.4) и затем эту ось приведем во вращение с угловой скоростью
’ вокруг оси ОА (рис.1.2.4) и затем эту ось приведем во вращение с угловой скоростью  0 вокруг неподвижной оси ОВ. Найдем результирующее движение тела. . Рис.1.2.4.
0 вокруг неподвижной оси ОВ. Найдем результирующее движение тела. . Рис.1.2.4.
За промежуток времени dt тело совершит поворот  вокруг
вокруг
оси АО и одновременно поворот d  ’ вокруг оси ОВ. Суммарный поворот, согласно (1.2.2), есть d
’ вокруг оси ОВ. Суммарный поворот, согласно (1.2.2), есть d  = d
= d  0 + d
0 + d  ’. Разделив обе части этого равенства на dt, получим
’. Разделив обе части этого равенства на dt, получим
 =
=  0 +
0 +  ’. (1.2.10)
’. (1.2.10)
Таким образом, результирующее движение твердого тела представляет собой чистое вращение с угловой скоростью 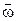 вокруг оси, совпадающей в каждый момент с этим вектором и проходящей через точку O (рис.1.2.4). Эта ось перемещается— она поворачивается с угловой скоростью
вокруг оси, совпадающей в каждый момент с этим вектором и проходящей через точку O (рис.1.2.4). Эта ось перемещается— она поворачивается с угловой скоростью  0 вместе с осью ОА вокруг оси ОВ.
0 вместе с осью ОА вокруг оси ОВ.
Нетрудно сообразить, что даже в том случае, когда угловые скорости ω’ и ω0 не меняются по модулю, тело будет обладать угловым ускорением 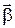 , направленным, согласно (1.2.4), перпендикулярно плоскости, проведенной через оси ОА и ОВ.
, направленным, согласно (1.2.4), перпендикулярно плоскости, проведенной через оси ОА и ОВ.
Дата добавления: 2015-08-08; просмотров: 3141;
