Вращение вокруг неподвижной оси. Пусть твердое тело, вращаясь вокруг неподвижной в данной системе отсчета оси OO’, совершило за время dt бесконечно малый поворот на угол

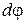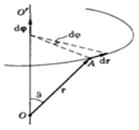
Пусть твердое тело, вращаясь вокруг неподвижной в данной системе отсчета оси OO’, совершило за время dt бесконечно малый поворот на угол . Чтобы характеризовать направление вращения, можно ввести вектор d , модуль которого равен углу поворота, а направление совпадает с осью OO’, причем так, что направление поворота связано правилом правого винта с направлением вектора d (рис.1.2.1).

Теперь найдем элементарное перемещение любой точки A

твердого тела при таком повороте. Положение точки A зададим

радиус-вектором , проведенным из некоторой точки O на оси вращения. Тогда линейное перемещение конца

радиус-вектора связано с углом поворота Рис.1.2.1.

dφ соотношением ,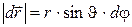

или в векторном виде

d = [d ]. (1.2.1)

Отметим, что это равенство справедливо лишь для бесконечно малого поворота d. Другими словами, только бесконечно малые повороты можно рассматривать как векторы.

Введенный нами вектор d удовлетворяет основному свойству векторов — векторному сложению. В самом деле, пусть твердое тело совершает два элементарных поворота d ₁ и d ₂ вокруг разных осей, проходящих через неподвижную точку O. Тогда результирующее перемещение произвольной точки A тела, радиус-вектор которой относительно точки O равен , можно представить так:

d = d ₁ + d ₂ = [d ₁, ] + [d ₂, ] = [d , ],

где

d =d ₁+d ₂, (1.2.2)

т. е. два данных поворота эквивалентны одному повороту вокруг оси, совпадающей с вектором d и проходящей через точку O.

Заметим, что при рассмотрении таких величин, как радиус-вектор, скорость, ускорение точки, не возникал вопрос о выборе их направления: оно вытекало естественным образом из природы самих величин. Подобные векторы называют полярными. В отличие от них векторы типа d , направление которых связывают с направлением вращения, называют аксиальными.

Введем векторы угловой скорости и углового ускорения. Вектор угловой скорости определяют как

=d /dt, (1.2.3)

где dt промежуток времени, за который тело совершает поворот d . Вектор совпадает по направлению с вектором d и представляет собой аксиальный вектор.

Изменение вектора со временем характеризуют вектором углового ускорения :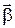

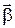=d /dt. (1.2.4)

Направление вектора 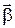совпадает с направлением d — приращением вектора . Вектор 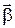, как и , является аксиальным.

Единицей угловой скорости в СИ является радиан в секунду (рад/с), а единицей углового ускорения — радиан на секунду в квадрате (рад/с²).

Представление угловой скорости и углового ускорения в виде векторов оказывается чрезвычайно плодотворным, особенно при изучении более сложных движений твердого тела. Это дает возможность во многих случаях получить большую наглядность, а также резко упростить как анализ движения, так и соответствующие расчеты.

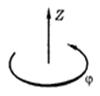
Запишем выражения для угловой скорости и углового ускорения в проекциях на ось вращения Z, положительное направление которой свяжем с положительным направлением отсчета координаты φ — угла поворота — правилом правого винта (рис.1.2.2). Тогда Рис.1.2.2.

проекции ω_z и β_z векторов и 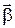на ось Z определяются формулами

(1.2.5)

(1.2.6)

Здесь ω_z и β_z — величины алгебраические. Их знак характеризует направление соответствующего вектора. Например, если ω_z > 0, то направление вектора совпадает с положительным направлением оси Z; если же ω_z < 0, то -противоположно. Аналогично и для углового ускорения.

Таким образом, зная зависимость φ(t) — закон вращения тела, по формулам (1.2.5) и (1.2.6) можно найти угловую скорость и угловое ускорение в каждый момент времени. И наоборот, если известны зависимость углового ускорения от времени и начальные условия, т. е. угловая скорость ω₀ и угол φ₀ в начальный момент времени, то можно найти ω (t) и φ(t).