Кинематика точки.

Чтобы описывать движение точки, нужно уметь задавать ее положение в пространстве. Положение интересующей нас точки A задают радиус-вектором , проведенным из некоторой неподвижной точки O выбранной системы отсчета (начало отсчета) в точку A. При движении точки A ее радиус-вектор меняется в общем Рис.1.1.1.

случае, как по модулю, так и по направлению, т. е.

радиус- вектор зависит от времени t. Геометрическое место концов радиус-вектора в данной системе отсчета называют траекторией точки A.

Введем понятие скорости точки. Пусть за промежуток времени Δt точка A переместилась из точки 1 в точку 2 (рис.1.1.1). Из рисунка видно, что вектор перемещения 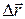точки A представляет собой приращение радиус-вектора за

время Δt: . Отношение Δ /Δt называют средним вектором скорости 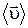за время Δt. Вектор 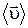совпадает по направлению с Δ .

Определим вектор скорости точки в данный момент

времени как предел отношения Δ /Δt при Δt → 0, т. е.

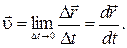(1.1.1)

Это значит, что вектор скорости точки в данный момент времени равен производной от радиус-вектора по времени и направлен по касательной к траектории в данной точке в сторону движения точки A (как и вектор d ). Модуль вектора равен

Движение точки характеризуется также ускорением. Вектор ускорения 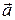определяет скорость изменения вектора скорости точки со временем:

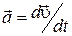(1.1.2)

т. е. равен производной от вектора скорости по времени. Направление вектора 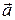совпадает с направлением вектора d — приращением вектора за время dt. Модуль вектора 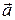определяется аналогично модулю вектора .

Таким образом, зная зависимость r(t), можно найти скорость и ускорение точки в каждый момент времени.

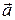Возникает и обратная задача: можно ли найти (t) и (t), зная зависимость от времени ускорения (t)?

Оказывается, для получения однозначного решения этой задачи одной зависимости 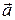(t) недостаточно, необходимо еще знать начальные условия, а именно скорость ₀ и радиус-вектор ₀ точки в некоторый начальный момент t = 0. Чтобы в этом убедиться, рассмотрим простейший случай, когда в процессе движения ускорение точки 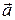= const. Такое движение называется равноускоренным.

Сначала определим скорость точки. Согласно (1.1.2), за промежуток времени dt элементарное приращение скорости d = 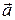dt. Проинтегрировав это выражение по времени от t = 0 до t, найдем приращение вектора скорости за это время:

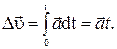
Но величина Δ — это еще не искомая скорость. Чтобы найти , необходимо знать скорость ₀ в начальный момент времени. Тогда = ₀ + Δ , или

= ₀ + 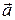t. (1.1.3)

Аналогично решается вопрос и о радиус-векторе точки. Согласно (1.1.1), за промежуток времени dt элементарное приращение радиус-вектора d =dt. Интегрируя это выражение с учетом найденной зависимости (t), определим приращение радиус-вектора за время от t = 0 до t:

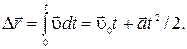
Для нахождения самого радиус-вектора (t) необходимо знать еще положение точки ₀ в начальный момент времени. Тогда = ₀ + Δ , или

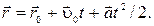(1.1.4)

Рассмотрим, например, движение камня, брошенного под некоторым углом к горизонту с начальной скоростью₀. Если считать, что камень движется с постоянным ускорением 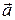= 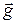, то его положение относительно точки бросания ( ₀ = 0) определяется радиус-вектором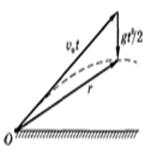

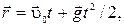
т. е. в данном случае представляет собой сумму двух векторов, что показано на рис.1.1.2.

Итак, для полного решения задачи о движении точки – оп ределения ее скорости и положения в зависимости от времени — недостаточно знать зависимость 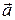(t), но еще необходимо знать и начальные условия, т. е. скорость ₀ и положение ₀ точки в начальный момент времени.

В заключение напомним, что в СИ единицами длины, скорости и ускорения являются соответственно метр (м), метр на секунду (м/с) и метр на секунду в квадрате (м/с²).

Можно с выбранным телом отсчета жестко связать определенную систему координат (декартову, косоугольную или криволинейную). Выбор той или иной системы координат определяется рядом соображений: характером или симметрией задачи, постановкой вопроса, а также стремлением упростить само решение. Ограничимся здесь декартовой системой координат x, y, z.Запишем проекции на оси x ,y ,z радиус-вектора (t), характеризующего положение интересующей нас точки относительно начала координат O в момент t: x=x(t); y=y(t); z=z(t).

Зная зависимость этих координат от времени — закон движения точки, можно найти положение точки в каждый момент времени, ее скорость и ускорение. Действительно, спроецировав (1.1.1) и (1.1.2), например, на ось x, получим формулы, определяющие проекции векторов скорости и ускорения на эту ось:

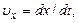(1.1.5)

где dx — проекция вектора перемещения d на ось x;

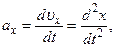(1.1.6)

где dυ_x — проекция вектора приращения скорости d на ось x. Аналогичные соотношения получаются для y- и z-проекций соответствующих векторов. Из этих формул видно, что проекции векторов скорости и ускорения равны соответственно первой и второй производным координат по времени.

Таким образом, зависимости x(t), y(t), z(t), по существу, полностью определяют движение точки. Зная их, можно найти не только положение точки, но и проекции ее скорости и ускорения, а, следовательно, модуль и направление векторов и 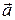в любой момент времени. Например, модуль вектора скорости

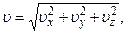(1.1.7)

направление же вектора задается направляющими косинусами по формулам

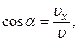
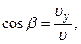
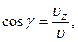
где α, β, γ — углы меду вектором и осями x, y, z соответственно. Аналогичными формулами определяются модуль и направление вектора ускорения.

Кроме того, можно решить и ряд других вопросов: найти траекторию точки, зависимость пройденного ею пути от времени, зависимость скорости от положения точки и пр.

Решение обратной задачи — нахождение скорости и закона движения точки по заданному ускорению — проводится, как и в векторном способе, путем интегрирования (в данном случае проекций ускорения по времени), причем задача и здесь имеет однозначное решение, если кроме ускорения заданы еще и начальные условия: проекции скорости и координаты точки в начальный момент.

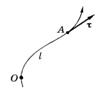Когда траектория точки известна, ее положение можно задать дуговой координатой l - расстоянием вдоль траектории от выбранного начала отсчета О (рис.1.1.3). При этом произвольно устанавливают положительное направление отсчета координаты l (например, так, как показано стрелкой на рисунке).

Движение точки определено, если известны ее траектория, начало отсчета O, положительное направление Рис.1.1.3.

отсчета дуговой координаты l и закон движения точки,

т. е. зависимость l(t).

Введем единичный вектор 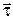, связанный с движущейся точкой A и направленный по касательной к траектории в сторону возрастания дуговой координаты l (рис.1.1.4).Очевидно, что 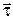— переменный по направлению вектор: он зависит от l. Вектор скорости точки A направлен по касательной к траектории, поэтому его можно представить так:

= υ_τ 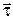, (1.1.8)

где υ_τ = dl/dt — проекция вектора на направление вектора 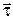, причем υ_τ — величина алгебраическая. Кроме того, | υ_τ | = | | = υ.

Продифференцируем (1.1.8) по времени:

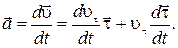(1.1.9)

Затем преобразуем второе слагаемое этого выражения:

(1.1.10)

Определим приращение вектора 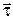на участке dl (рис.1.1.4). Можно строго показать, что при стремлении точки 2 к точке 1 отрезок траектории между ними стремится к дуге окружности с центром в некоторой точке O. Эту точку называют центром кривизны траектории в данной точке, а радиус ρ соответствующей окружности — радиусом кривизны траектории в той же точке.

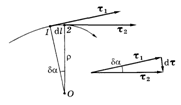Как видно из рисунка, угол 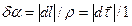, откуда Рис.1.1.4.

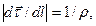причем, если dl → 0, то d 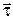^ 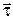. Введя единичный вектор нормали к траектории в точке 1, направленный к центру кривизны, запишем последнее равенство в векторном виде:

d 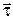/dl = /ρ. (1.1.11)

Подставим (1.1.11) в (1.1.10) и полученное выражение в (1.1.9). В результате найдем

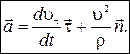(1.1.12)

Здесь первое слагаемое называют тангенциальным ускорением, второе — нормальным ускорением. Таким образом, полное ускорение точки может быть представлено как векторная сумма тангенциального и нормального ускорений.

Проекции вектора 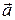на орты 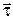и , как видно из (1.1.12), равны

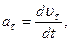
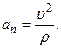(1.1.13)

Модуль полного ускорения точки

.

Отметим, что за счет тангенциального ускорения скорость меняется по модулю, а за счет нормального – по направлению.