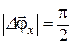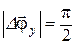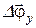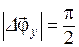Вращательное движение материальной точки
Различают два вида вращательного движения материальной точки:
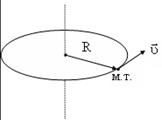
– вращательное движение вокруг неподвижной оси – это движение материальной точки по окружности радиуса R, центр которой лежит на неподвижной относительно данной системы отсчета прямой (ось вращения), перпендикулярной плоскости, в которой лежит траектория точки (рис. 1.6а);
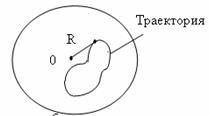
– вращательное движение около неподвижной точки – это движение материальной точки по поверхности сферы радиуса R, центр которой лежит в некоторой неподвижной относительно данной системы точке О (рис. 1.6б).
 а)
а)
|
 б)
б)
| В этом случае в каждый момент времени материальная точка вращается вокруг так называемой мгновенной оси вра-щения, которая проходит через точку О и изменяет с течением времени свою ориентацию относительно осей координат системы отсчета.
|
| Рис. 1.6
|
Для характеристики вращательного движения вводят угловые кинематические величины: угол поворота; угловую скорость; угловое ускорение.
Пусть материальная точка вращается по окружности радиуса R с центром в точке С (рис. 1.7). Положение материальной точки на окружности в произволь-
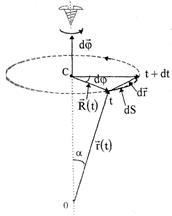 Рис.1.7
Рис.1.7
| ный момент времени t можно охарактеризовать радиус-вектором 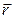 , проведенным из некоторой точки О, лежащей на мгновенной оси вращения и выбранной в качестве точки отсчета. Изменение положения материальной точки за промежуток времени dt, то есть ее перемещение , проведенным из некоторой точки О, лежащей на мгновенной оси вращения и выбранной в качестве точки отсчета. Изменение положения материальной точки за промежуток времени dt, то есть ее перемещение 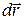 , связано с углом поворота dj радиуса окружности , связано с углом поворота dj радиуса окружности 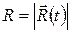 , скрепленного с материальной точкой. Из рис. 1.7 видно, что , скрепленного с материальной точкой. Из рис. 1.7 видно, что
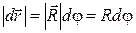 ,
где ,
где 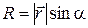 , то есть , то есть
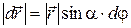 . (1.26) . (1.26)
|
Этому соотношению можно придать векторную форму, если ввести вектор 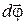 – вектор угла поворота, направление которого связано с направлением вращения материальной точки определенным правилом.
– вектор угла поворота, направление которого связано с направлением вращения материальной точки определенным правилом.
Условились для определения этой связи применять правило правого винта: вектор 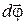 направлять по мгновенной оси вращения в ту сторону, куда будет двигаться винт с правой нарезкой, при вращении его головки в сторону вращения материальной точки (рис 1.7).
направлять по мгновенной оси вращения в ту сторону, куда будет двигаться винт с правой нарезкой, при вращении его головки в сторону вращения материальной точки (рис 1.7).
Теперь
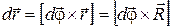 . (1.27)
. (1.27)
Здесь и ниже скобками [ ] обозначено векторное произведение векторов.
Следует отметить, что из-за условности выбора направления угла поворота 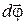 свойства этого вектора (и ему подобных) существенным образом отличаются от обычных векторов. Поэтому их называют псевдовекторами или аксиальными векторами.
свойства этого вектора (и ему подобных) существенным образом отличаются от обычных векторов. Поэтому их называют псевдовекторами или аксиальными векторами.
В частности последовательные бесконечно малые повороты, характеризуемые векторами 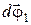 и
и 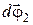 , при их сложении дают результирующий поворот
, при их сложении дают результирующий поворот 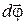 , равный
, равный
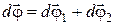 ,
,
то есть подчиняются обычному правилу сложения векторов. Для поворотов, характеризуемых конечными углами 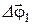 и
и  , их геометрическая сумма не равна результирующему повороту
, их геометрическая сумма не равна результирующему повороту 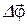 , то есть
, то есть
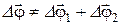 .
.
Более того, из наглядного примера (см. рис. 1.8) видно, что
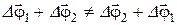 .
.
Рис. 1.8
Скорость поворота характеризуется с помощью понятия угловой скорости  в данный момент времени t (мгновенной угловой скорости):
в данный момент времени t (мгновенной угловой скорости):
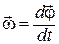 . (1.28)
. (1.28)
Вектор мгновенной угловой скорости  ориентирован так же, как и
ориентирован так же, как и 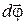 ,
,
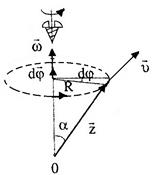
вдоль мгновенной оси вращения, и связан правилом правого винта с направлением вращения в данный момент времени. Поэтому  является аксиальным вектором (рис. 1.9а,б). При вращении вокруг неподвижной оси вектор
является аксиальным вектором (рис. 1.9а,б). При вращении вокруг неподвижной оси вектор  направлен вдоль этой оси. При вращении вокруг неподвижной точки
направлен вдоль этой оси. При вращении вокруг неподвижной точки  изменяет
изменяет
| 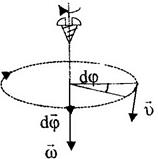
| свое направление вместе с изменением ориентации мгновенной оси.
Если в процессе вращения угловая скорость  является функцией времени, то для характеристики быстроты изменения является функцией времени, то для характеристики быстроты изменения  как по величине, так и по направлению, вводят угловое ускорение: как по величине, так и по направлению, вводят угловое ускорение:
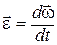 . (1.29)
Направление вектора . (1.29)
Направление вектора 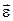 опреде- опреде-
|
| а)
| б)
|
| Рис. 1.9
|
ляется направлением 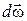 в данный момент времени. При вращении материальной точки вокруг неподвижной оси угловое ускорение направлено вдоль этой оси.
в данный момент времени. При вращении материальной точки вокруг неподвижной оси угловое ускорение направлено вдоль этой оси.
При этом 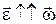 ,
,  ,
,  , если
, если 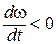 .
.
Выводы: При вращении материальной точки ее движение может описываться с помощью угловых кинематических величин: угла поворота 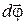 , угловой скорости
, угловой скорости  и углового ускорения
и углового ускорения 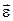 , которые являются аксиальными векторами. При вращении вокруг неподвижной оси
, которые являются аксиальными векторами. При вращении вокруг неподвижной оси 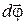 ,
,  и
и 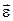 направлены вдоль этой оси. При вращении вокруг неподвижной точки
направлены вдоль этой оси. При вращении вокруг неподвижной точки 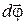 и
и  направлены вдоль мгновенной оси вращения, а
направлены вдоль мгновенной оси вращения, а 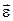 сонаправлен с приращением
сонаправлен с приращением 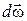 в данный момент времени.
в данный момент времени.
Контрольные вопросы
1.9. Каков смысл вектора 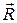 в соотношении (1.27), если ось вращения изменяет с течением времени свою ориентацию?
в соотношении (1.27), если ось вращения изменяет с течением времени свою ориентацию?
1.10. Охарактеризуйте вращательное движение материальной точки, соответствующее условиям: а)  ; б)
; б) 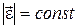 ; в)
; в) 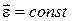 ; г)
; г) 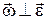 ,
, 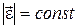 .
.
Дата добавления: 2015-08-08; просмотров: 1704;
 а)
а)
 б)
б)
 Рис.1.7
Рис.1.7
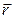 , проведенным из некоторой точки О, лежащей на мгновенной оси вращения и выбранной в качестве точки отсчета. Изменение положения материальной точки за промежуток времени dt, то есть ее перемещение
, проведенным из некоторой точки О, лежащей на мгновенной оси вращения и выбранной в качестве точки отсчета. Изменение положения материальной точки за промежуток времени dt, то есть ее перемещение 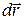 , связано с углом поворота dj радиуса окружности
, связано с углом поворота dj радиуса окружности 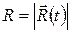 , скрепленного с материальной точкой. Из рис. 1.7 видно, что
, скрепленного с материальной точкой. Из рис. 1.7 видно, что
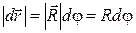 ,
где
,
где 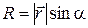 , то есть
, то есть
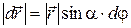 . (1.26)
. (1.26)
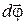 – вектор угла поворота, направление которого связано с направлением вращения материальной точки определенным правилом.
– вектор угла поворота, направление которого связано с направлением вращения материальной точки определенным правилом.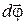 направлять по мгновенной оси вращения в ту сторону, куда будет двигаться винт с правой нарезкой, при вращении его головки в сторону вращения материальной точки (рис 1.7).
направлять по мгновенной оси вращения в ту сторону, куда будет двигаться винт с правой нарезкой, при вращении его головки в сторону вращения материальной точки (рис 1.7).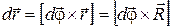 . (1.27)
. (1.27)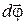 свойства этого вектора (и ему подобных) существенным образом отличаются от обычных векторов. Поэтому их называют псевдовекторами или аксиальными векторами.
свойства этого вектора (и ему подобных) существенным образом отличаются от обычных векторов. Поэтому их называют псевдовекторами или аксиальными векторами.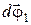 и
и 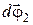 , при их сложении дают результирующий поворот
, при их сложении дают результирующий поворот 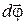 , равный
, равный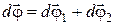 ,
,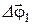 и
и  , их геометрическая сумма не равна результирующему повороту
, их геометрическая сумма не равна результирующему повороту 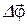 , то есть
, то есть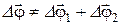 .
.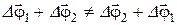 .
.





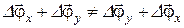
 в данный момент времени t (мгновенной угловой скорости):
в данный момент времени t (мгновенной угловой скорости):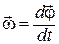 . (1.28)
. (1.28) ориентирован так же, как и
ориентирован так же, как и 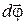 ,
, является аксиальным вектором (рис. 1.9а,б). При вращении вокруг неподвижной оси вектор
является аксиальным вектором (рис. 1.9а,б). При вращении вокруг неподвижной оси вектор  направлен вдоль этой оси. При вращении вокруг неподвижной точки
направлен вдоль этой оси. При вращении вокруг неподвижной точки  изменяет
изменяет

 является функцией времени, то для характеристики быстроты изменения
является функцией времени, то для характеристики быстроты изменения  как по величине, так и по направлению, вводят угловое ускорение:
как по величине, так и по направлению, вводят угловое ускорение:
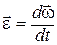 . (1.29)
Направление вектора
. (1.29)
Направление вектора 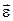 опреде-
опреде-
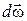 в данный момент времени. При вращении материальной точки вокруг неподвижной оси угловое ускорение направлено вдоль этой оси.
в данный момент времени. При вращении материальной точки вокруг неподвижной оси угловое ускорение направлено вдоль этой оси. 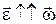 ,
,  ,
,  , если
, если 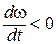 .
.
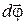 , угловой скорости
, угловой скорости  и углового ускорения
и углового ускорения 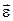 , которые являются аксиальными векторами. При вращении вокруг неподвижной оси
, которые являются аксиальными векторами. При вращении вокруг неподвижной оси 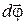 ,
,  и
и 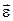 направлены вдоль этой оси. При вращении вокруг неподвижной точки
направлены вдоль этой оси. При вращении вокруг неподвижной точки 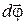 и
и  направлены вдоль мгновенной оси вращения, а
направлены вдоль мгновенной оси вращения, а 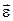 сонаправлен с приращением
сонаправлен с приращением 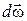 в данный момент времени.
в данный момент времени.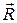 в соотношении (1.27), если ось вращения изменяет с течением времени свою ориентацию?
в соотношении (1.27), если ось вращения изменяет с течением времени свою ориентацию? ; б)
; б) 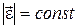 ; в)
; в) 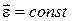 ; г)
; г) 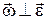 ,
, 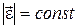 .
.