Радиус-вектор, вектор перемещения
Для описания движения материальной точки в каждый момент времени необходимо указать ее положение относительно выбранной системы отсчета. Для этого с телом отсчета связывают систему координат – способ, с помощью которого задают числа (координаты точки), полностью определяющие положение материальной точки относительно тела отсчета. Важнейшими системами координат являются прямоугольные декартовы системы координат (рис 1.1), в которых положение точки А однозначно определяется ее координатами x, y, z
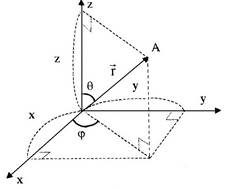 Рис. 1.1
Рис. 1.1
| по отношению к началу координат О, связанному с телом отсчета.
Поскольку тело отсчета и материальная точка определяют в пространстве физически выделенное направление OA, то положение материальной точки в данной системе координат (XYZ) можно характеризовать одной векторной величиной 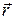 – радиус-вектором. Задать радиус-вектор положения материальной точки А – означает: указать, на каком расстоянии от тела отсчета (модуль радиус-вектора – радиус-вектором. Задать радиус-вектор положения материальной точки А – означает: указать, на каком расстоянии от тела отсчета (модуль радиус-вектора 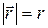 ) и в каком направлении относительно выбранных координатных ) и в каком направлении относительно выбранных координатных
|
направлений (полярный – j и азимутальный – q углы) находится материальная точка А.
Из рис. 1.1 непосредственно видно, что проекции радиус-вектора 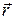 на оси координат определяют координаты материальной точки x, y, z.
на оси координат определяют координаты материальной точки x, y, z.
Преимущество векторного способа описания проявляется в том, что он компактнее координатного. Однако необходимо четко понимать, что векторный способ описания положения точки требует задания трех чисел: r, j, q так же, как и координатный.
Зная координаты точки x, y, z, нетрудно получить значения r, j, q:
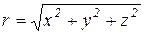 ,
, 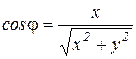 ,
, 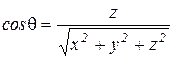 , (1.1)
, (1.1)
где cosj, cosq – направляющие косинуса радиус-вектора 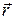 .
.
Если известны числа r, j, q, то координаты x, y, z частицы определяются соотношениями:
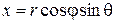 ,
, 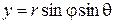 ,
, 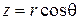 . (1.2)
. (1.2)
При движении материальной точки ее положение относительно начала координат с течением времени изменяется, а следовательно может изменяться как модуль, так и направление радиус-вектора 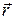 .
.
Следовательно, радиус-вектор является функцией времени:
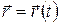 ,
, 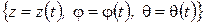
или
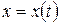 ,
, 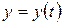 ,
, 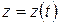 . (1.3)
. (1.3)
Эти функции, которые однозначно определяют характер и вид движения частицы, называются кинематическими уравнениями движения материальной точки. При этом конец радиус-вектора описывает в пространстве линию – траекторию движения.
Изменение положения материальной точки при ее движении из некоторого начального положения в момент времени t, характеризуемого радиус-вектором 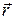 , в другое положение в момент времени
, в другое положение в момент времени 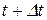 , характеризуемого радиус-вектором
, характеризуемого радиус-вектором 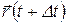 , определяется вектором
, определяется вектором 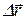 , который называется вектором
, который называется вектором
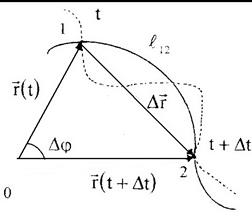 Рис. 1.2
Рис. 1.2
| перемещения (рис. 1.2).
Здесь следует четко понять, что вектор перемещения характеризует результирующее изменение положения материальной точки за промежуток времени 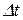 , и не содержит в себе информации ни о виде траектории, ни о характере движения по ней. Кроме этого, даже из рисунка следует, что величина перемещения , и не содержит в себе информации ни о виде траектории, ни о характере движения по ней. Кроме этого, даже из рисунка следует, что величина перемещения 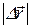 , путь S12, пройденный материальной точкой, и длина дуги траектории l12, заключенной между положениями 1 и 2, в общем случае , путь S12, пройденный материальной точкой, и длина дуги траектории l12, заключенной между положениями 1 и 2, в общем случае
|
различны по величине, то есть
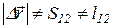 . (1.4)
. (1.4)
Выводы: Положение материальной точки в выбранной системе отсчета, характеризуется радиус-вектором. При движении частицы ее радиус-вектор изменяется. Закон этого изменения с течением времени полностью определяет вид траектории частицы и характер движения по ней. Вектор перемещения описывает изменение положения за данный промежуток времени.
Контрольные вопросы
1.2. Охарактеризуйте движения частицы, соответствующие соотношениям а) 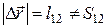 , б)
, б) 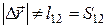 .
.
1.3. Используя рис.1.1, убедитесь в справедливости соотношений (1.1) и (1.2).
Дата добавления: 2015-08-08; просмотров: 1566;
