Інтеграл Лебега по множині нескінченної міри.
Нехай 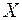 -довільна непорожня множина і на
-довільна непорожня множина і на 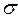 -алгебрі
-алгебрі 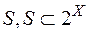 , визначена
, визначена 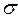 -скінченна міра
-скінченна міра 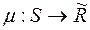 , причому
, причому 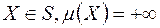 . Тоді існує така послідовність
. Тоді існує така послідовність 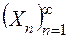 множин
множин 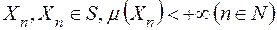 , що
, що
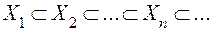 ,
,
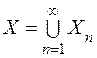 .
.
Кожна послідовність  -вимірних множин, яка володіє вказаними вище властивостями, називається вичерпною послідовністю для множини
-вимірних множин, яка володіє вказаними вище властивостями, називається вичерпною послідовністю для множини  .
.
Нехай на множині 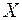 визначена
визначена 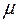 -вимірна функція
-вимірна функція 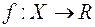
Означення. Функція 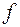 називається інтегровною за Лебегом (
називається інтегровною за Лебегом ( 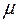 -інтегровною або сумовною) на множині
-інтегровною або сумовною) на множині 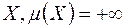 , якщо вона інтегровна за Лебегом на кожній
, якщо вона інтегровна за Лебегом на кожній 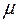 -вимірній множині
-вимірній множині 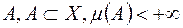 , і для кожної вичерпної для
, і для кожної вичерпної для 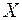 послідовності
послідовності 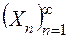 існує скінченна границя
існує скінченна границя
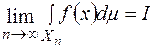 . (1)
. (1)
Вказана границя називається інтегралом Лебега від функції 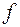 по множині
по множині 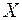 і позначається
і позначається 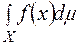 тобто
тобто
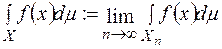 .
.
Можна показати, що границя (1), якщо вона існує скінченна для кожної вичерпної послідовності 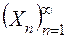 , не залежить від вибору такої послідовності тобто, що сформульоване вище означення коректне.
, не залежить від вибору такої послідовності тобто, що сформульоване вище означення коректне.
Зауваження 1. Для функції 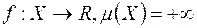 , такої, що
, такої, що 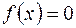 , коли
, коли 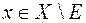 , де
, де 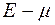 -вимірна множина,
-вимірна множина, 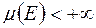 , сформульоване вище означення інтеграла Лебега по множині
, сформульоване вище означення інтеграла Лебега по множині 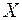 , рівносильне означенню інтеграла Лебега по множині
, рівносильне означенню інтеграла Лебега по множині 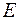 , яке було сформульовано раніше.
, яке було сформульовано раніше.
Зауваження 2. Зазначимо, що більшість тверджень, які були сформульовані для інтеграла Лебега по множині 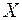 із скінченним значенням міри,
із скінченним значенням міри, 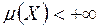 , залишаються в силі і у випадку, коли
, залишаються в силі і у випадку, коли 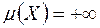 .
.
Суттєва відмінність полягає лише в тому, що у випадку, коли 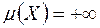 , обмежена і
, обмежена і 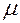 -вимірна на множині
-вимірна на множині 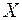 функція
функція 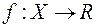 не обов'язково повинна бути інтегровною за Лебегом на
не обов'язково повинна бути інтегровною за Лебегом на 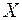 . Зокрема стала
. Зокрема стала 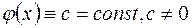 , не є інтегровною за Лебегом на множині
, не є інтегровною за Лебегом на множині 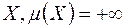 , оскільки для довільної вичерпної для
, оскільки для довільної вичерпної для 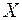 послідовності
послідовності 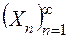 буде
буде
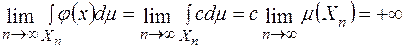 .
.
Зазначимо також, що теореми Лебега, Фату, Б. Леві, які торкаються граничного переходу під знаком інтеграла Лебега, справедливі і у випадку, коли 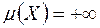 .
.
Дата добавления: 2015-07-24; просмотров: 736;
