Визначення поверхневого інтегралу ІІ типу

Лекція 47. Поверхневі інтеграли ІІ типу

План

1. Визначення поверхневого інтегралу ІІ типу
2. Обчислення поверхневого інтегралу ІІ типу
3. Обчислення обєму тіла за допомогою поверхневого інтегралу

Визначення поверхневого інтегралу ІІ типу

Нехай 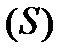- двобічна поверхня, яка визначена явно рівнянням:

.

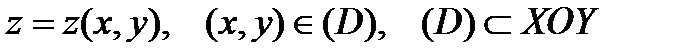Зафіксуємо якийсь її бік. Оскільки поверхня задана явно, то це може бути нижня чи верхня сторона поверхні (рис.1).Оберемо верхню сторону. Тоді додатний напрямок обходу замкненої кривої на верхньому боці поверхні відповідає додатному напрямку обходу проекції на ХОУ. Така проекція буде розглядатися із знаком «+». Для нижньої сторони поверхні 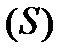все буде навпаки: додатному напрямку обходу замкненої кривої поверхні відповідає відємний напрямок обходу проекції на ХОУ. Така проекція буде мати знак «-» (рис.1,2).

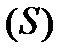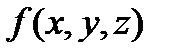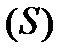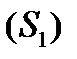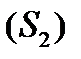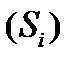Нехай на визначена функція . Розібємо гладкими кривими на , , ..., . На кожній частці оберемо довільно проміжкову точку 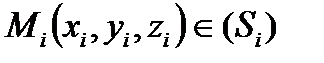. Побудуємо

,

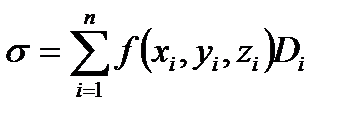де 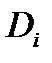- площа проекції підповерхні 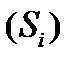з потрібним знаком, яка називається інтегральною сумою для поверхневого інтеграла ІІ типа.

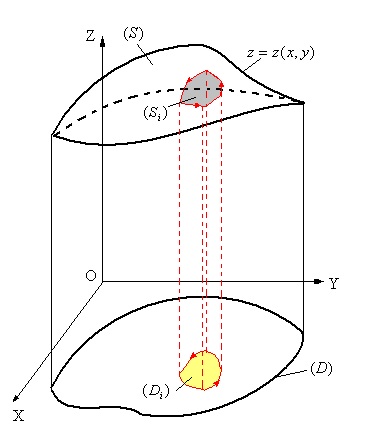
Рис.1.

Позначимо

.

Визначення. Якщо існує

,

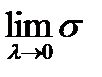яка не залежить ні від того, як поверхня 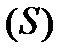розбивалася на частки 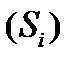, ні від вибору проміжкових точок, то ця границя називається поверхневим інтегралом ІІ типу від 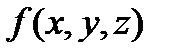по 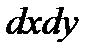, який відповідає обраній стороні поверхні і позначається:

.

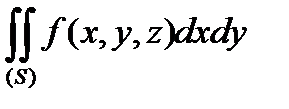Зауваження. Якщо змінити сторону поверхні, інтеграл 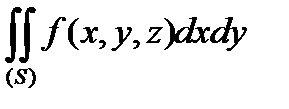змінить знак.

Якщо при побудові інтегральної суми проекції 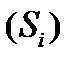будуються не на ХОУ, а на XOZ(YOZ), то отримаємо два інших поверхневих інтеграли ІІ типу:

( ).

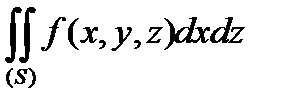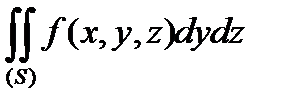Нехай на поверхні 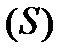визначені функції 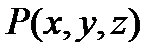, , 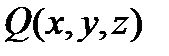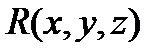. Тоді сума

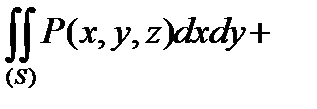
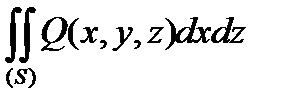
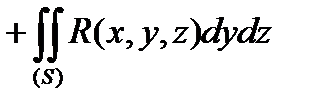
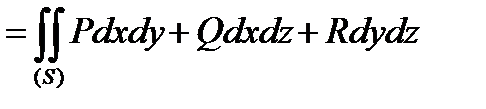
Називається поверхневим інтегралом ІІ типу загального виду.

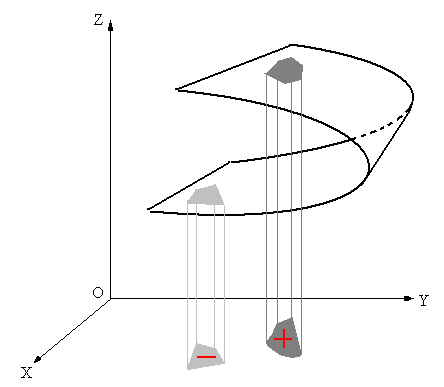
Рис.2.