Обчислення поверхневого інтегралу ІІ типу
Нехай поверхня 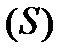 визначена явно:
визначена явно: 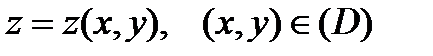 . До того ж
. До того ж  - неперервні в
- неперервні в 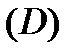 . Розглянемо
. Розглянемо 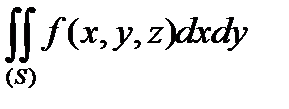 , який береться по верхній стороні поверхні. Тоді в інтегральній сумі
, який береться по верхній стороні поверхні. Тоді в інтегральній сумі  всі
всі  додатні:
додатні:
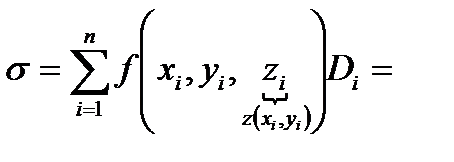
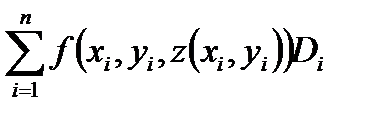 . (1)
. (1)
Права частина отриманої рівності – це інтегральна сума для подвійного інтегралу 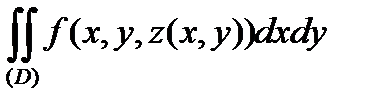 .
.
Якщо в рівності (1) перейти до границі, коли  , то отримаємо:
, то отримаємо:
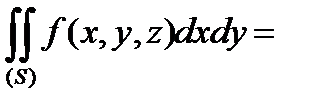
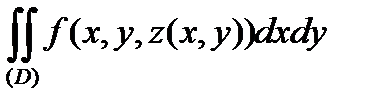 ,
,
до того ж існування одного з інтегралів веде до існування іншого.
Якщо поверхневий інтеграл обчислюється по нижній стороні поверхні 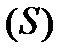 , то
, то
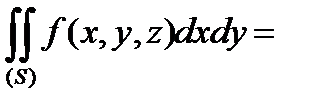
 .
.
Зауваження. Якщо 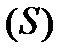 - частка циліндричної поверхні з твірною, паралельною осі OZ, то
- частка циліндричної поверхні з твірною, паралельною осі OZ, то
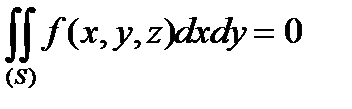 .
.
Дата добавления: 2015-08-21; просмотров: 569;
