Визначення та властивості криволінійного інтегралу ІІ роду

Нехай

.

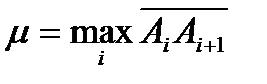Якщо при 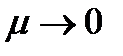сума (20) має скінченну границю

,

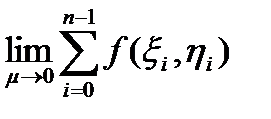
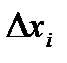яка не залежить ні від способу розбивки 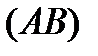на частки 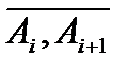, ні від вибору проміжкових точок 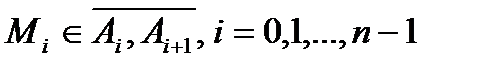, то ця границя називається криволінійним інтегралом ІІ роду від 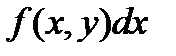по кривій 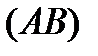і позначається:

.

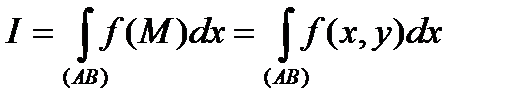Аналогічно, якщо помножити 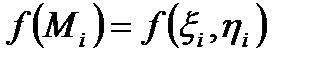не на , а на 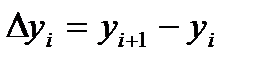і побудувати суму

= ,

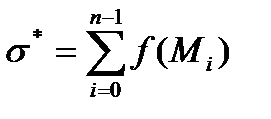
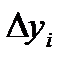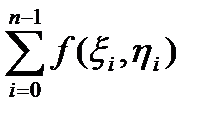
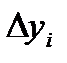то

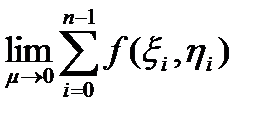
дасть нам криволінійний інтеграл ІІ роду від :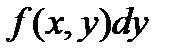

.

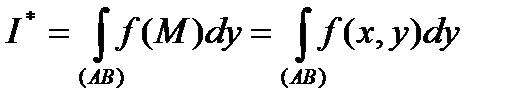Якщо вздовж кривої 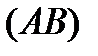визначені дві функції 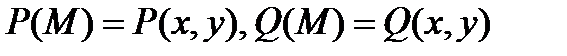і існують:

, ,

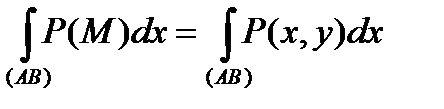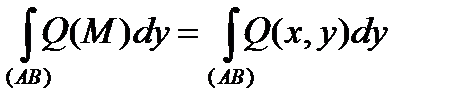то їх суму називають криволінійним інтегралом ІІ роду загального виду і позначають:

.

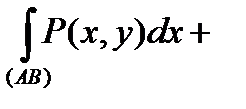
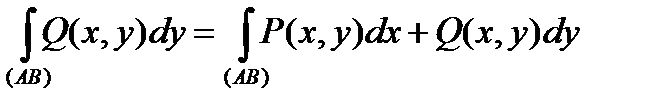Зауваження. Значенні криволінійного інтеграла ІІ роду залежить від напрямку, який обрано на кривій:

,

,

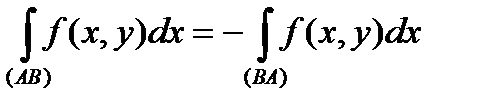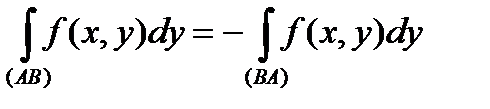до того ж з існування інтеграла зправа витікає існування інтеграла зліва і навпаки.

Аналогічно визначається криволінійний інтеграл ІІ роду по кривій, яка знаходиться не на площині, а в тривимірному просторі.