Існування та обчислення криволінійного інтегралу ІІ роду
Нехай крива 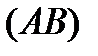 визначена параметрично:
визначена параметрично:
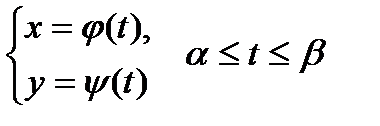 , (25)
, (25)
функції 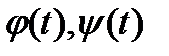 - неперервні, при зміні параметру від
- неперервні, при зміні параметру від 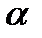 до
до  крива визначається в напрямку від
крива визначається в напрямку від 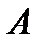 до
до 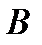 ;
; 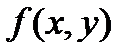 і
і 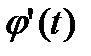 вздовж
вздовж 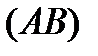 неперервні.
неперервні.
Теорема. При зроблених припущеннях криволінійний інтеграл ІІ роду 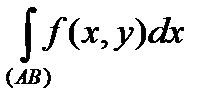 існує і
існує і
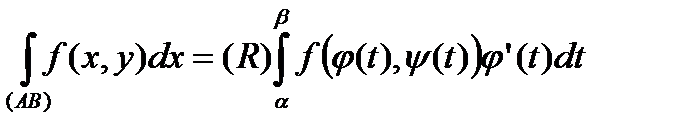 . (30)
. (30)
Порядок розташування границь інтегрування відповідає обраному на кривій напрямку.
Доказ. Нехай точки  , визначаються значеннями параметру
, визначаються значеннями параметру 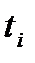 , а обрані на дугах
, а обрані на дугах 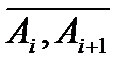 точки
точки 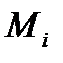 ,
, 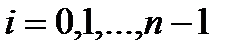 , значеннями параметру, які позначимо через
, значеннями параметру, які позначимо через 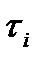
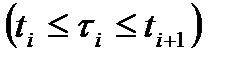 . Тоді інтегральна сума
. Тоді інтегральна сума 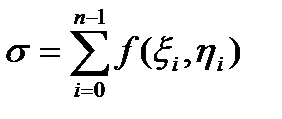
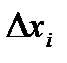 , якщо врахувати, що
, якщо врахувати, що
 ,
,
може бути записана у вигляді:
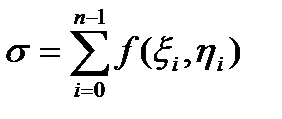
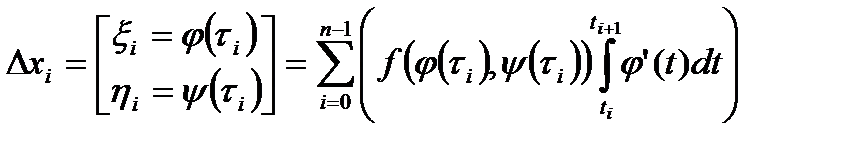 . (40)
. (40)
З іншого боку, інтеграл в (30) справа можна представити наступним чином:
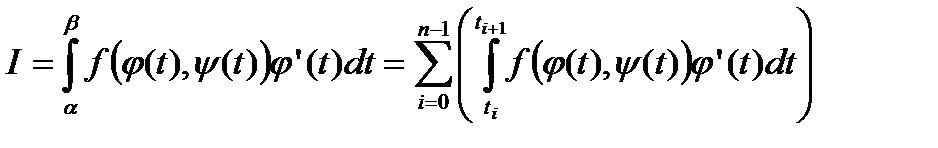 . (50)
. (50)
Тоді, враховуючи (40),(50), отримаємо:
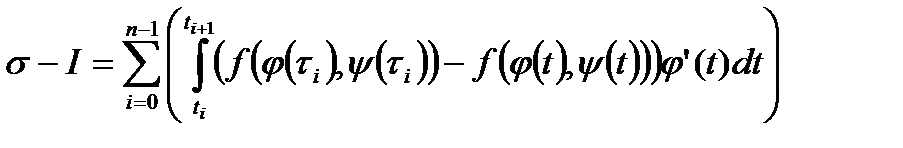 (60)
(60)
Візмемо 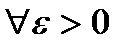 . Оскільки
. Оскільки 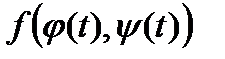 неперервна на
неперервна на 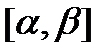 , то вона рівномірно неперервна на
, то вона рівномірно неперервна на 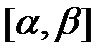 , тому
, тому 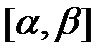 можна розбити на частки
можна розбити на частки 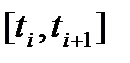 так, щоб на кожному частковому сегменті
так, щоб на кожному частковому сегменті 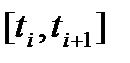 коливання функції
коливання функції 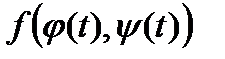 були меньше за
були меньше за 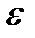 . Функція
. Функція 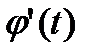 неперервна на
неперервна на 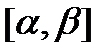 , тому
, тому 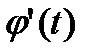 обмежена на
обмежена на 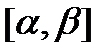 , тобто
, тобто 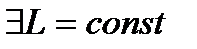 така, що
така, що 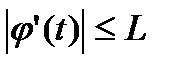 для
для 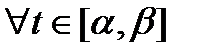 . Тоді
. Тоді
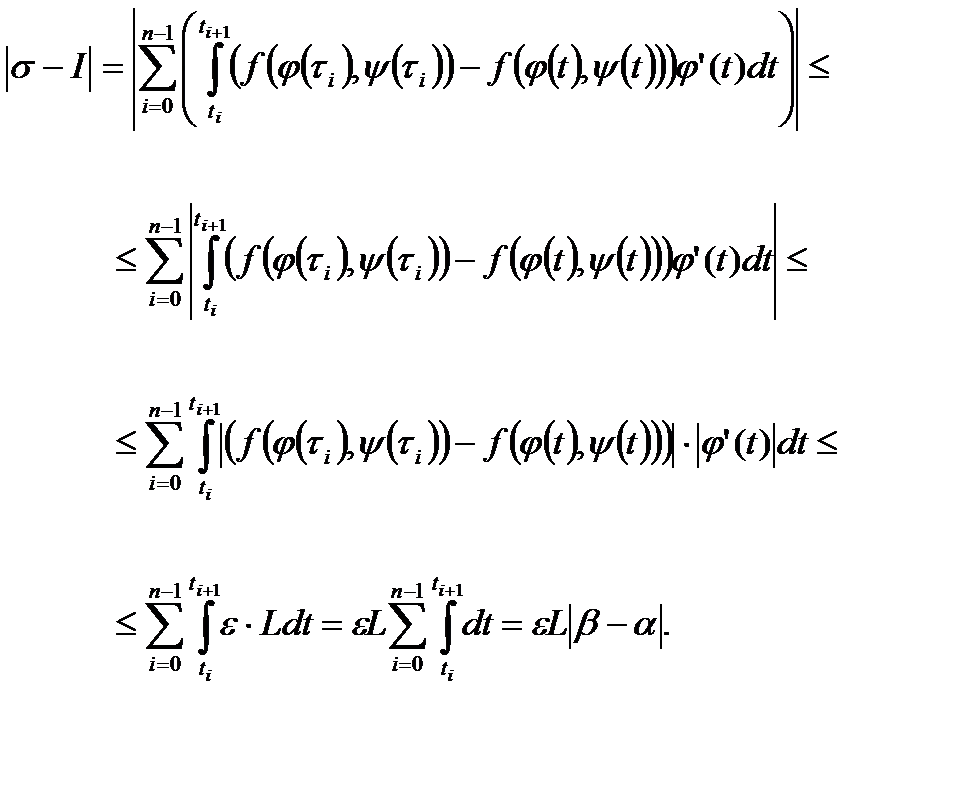 (70)
(70)
Позначимо
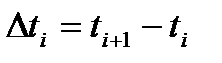 ,
, 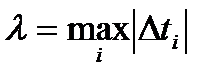 ,
,
тоді з (70) витікає, що
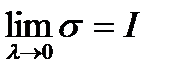 ,
,
що і треба було довести.
Аналогічно, якщо крива 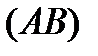 визначена за допомогою (25), функції
визначена за допомогою (25), функції 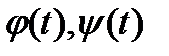 - неперервні, при зміні параметру від
- неперервні, при зміні параметру від 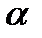 до
до  крива визначається в напрямку від
крива визначається в напрямку від 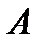 до
до 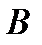 ;
; 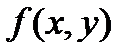 і
і 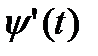 вздовж
вздовж 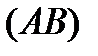 неперервні, то
неперервні, то
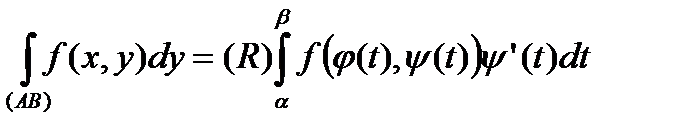 .
.
Порядок розташування границь інтегрування відповідає обраному на кривій напрямку.
Якщо крива 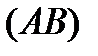 визначена за допомогою (25), функції
визначена за допомогою (25), функції 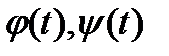 - неперервні, при зміні параметру від
- неперервні, при зміні параметру від 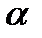 до
до  крива визначається в напрямку від
крива визначається в напрямку від 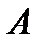 до
до 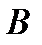 ;
; 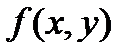 ,
, 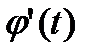
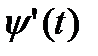 вздовж
вздовж 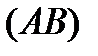 неперервні, то криволінійний інтеграл ІІ роду загального виду обчислюється за формулою:
неперервні, то криволінійний інтеграл ІІ роду загального виду обчислюється за формулою:
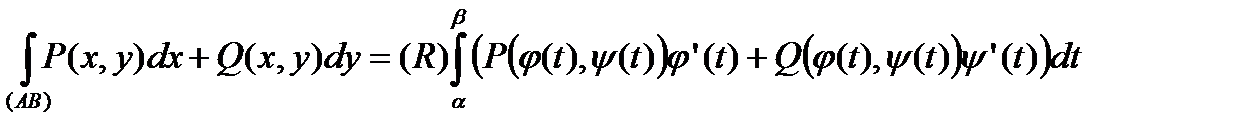 .
.
Нехай криволінійний інтеграл ІІ роду береться по кривій, яка визначається за допомогою рівняння
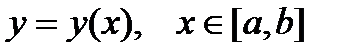 , (80)
, (80)
тоді формула (30) приймає вид:
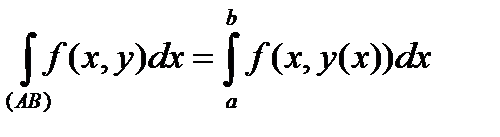 . (90)
. (90)
Приклад. Обчислити криволінійний інтеграл ІІ роду 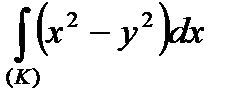 , де
, де 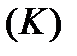 визначається наступним чином:
визначається наступним чином: 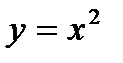 , що проходиться від точки з абсцисою
, що проходиться від точки з абсцисою 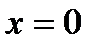 до точки з абсцисою
до точки з абсцисою 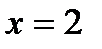 .
.
Відповідно до формули (90) маємо:
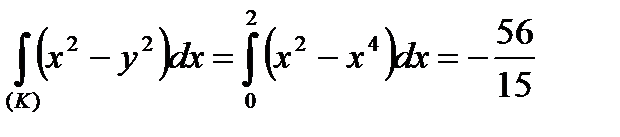 .
.
Зауваження 1. Криволінійний інтеграл ІІ роду 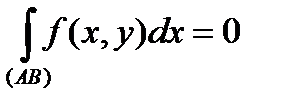
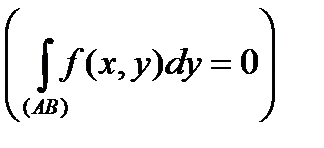 , якщо крива
, якщо крива 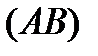 - це відрізок, паралельний осі ОУ (відрізок, паралельний осі ОХ).
- це відрізок, паралельний осі ОУ (відрізок, паралельний осі ОХ).
Зауваження 2. Нехай точка 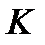 належить кривій
належить кривій 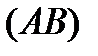 , тоді:
, тоді:
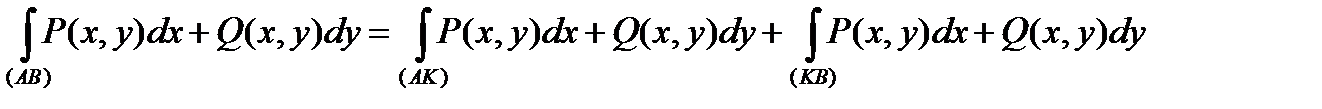 .
.
Дата добавления: 2015-08-21; просмотров: 1002;
