Побудова інтегральної суми для криволінійного інтегралу ІІ роду

Лекція 42. Криволінійні інтеграли ІІ роду

План

1. Побудова інтегральної суми для криволінійного інтегралу ІІ роду
2. Визначення та властивості криволінійного інтегралу ІІ роду
3. Існування та обчислення криволінійного інтегралу ІІ роду
4. Випадок замкненої кривої. Орієнтація площини

Побудова інтегральної суми для криволінійного інтегралу ІІ роду

Нехай задана неперервна крива 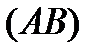(яку ми для простоти спочатку припустимо незамкненою), і нехай вздовж неї визначена деяка функція 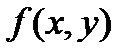. Розібємо криву 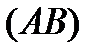точками 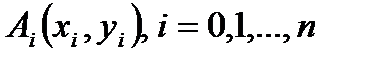, на часткові дуги 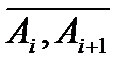. На кожній дузі 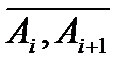, , 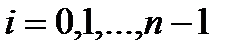оберемо довільно точки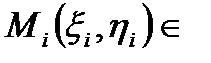 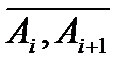. Обчислимо в кожній точці 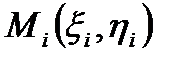значення функції 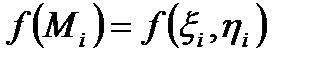, але ці значення будемо множити не на довжину відповідної часткової дуги 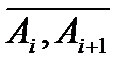, а на значення проекції цієї дуги на вісь ОХ (рис.1), тобто на

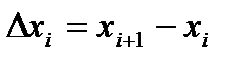. (10)

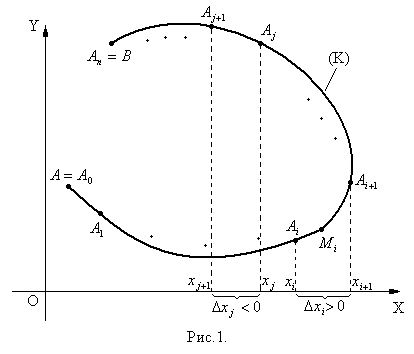
Побудуємо суму, яку назвемо інтегральною сумою для криволінійного інтегралу ІІ роду:

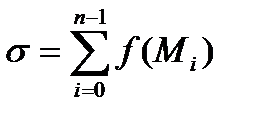
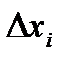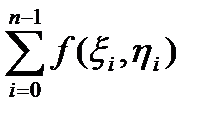
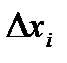= . (20)