Зведення криволінійного інтегралу І роду до інтегралу Римана
Припустимо, що на кривій  обрано напрямок від
обрано напрямок від 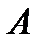 до
до  (один з двох можливих). Тоді положення довільної точки
(один з двох можливих). Тоді положення довільної точки  на кривій може бути визначено не тільки її координатами
на кривій може бути визначено не тільки її координатами 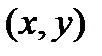 , а і довжиною дуги
, а і довжиною дуги  , яка відраховується від початкової точки
, яка відраховується від початкової точки 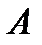 . Тоді крива
. Тоді крива 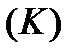 може бути параметрично визначена наступним чином:
може бути параметрично визначена наступним чином:
 ,
,
де  - довжина всієї кривої
- довжина всієї кривої  . Функція
. Функція  , яка визначена вздовж кривої
, яка визначена вздовж кривої 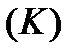 , зведеться до складної функції
, зведеться до складної функції  від змінної
від змінної  .
.
Позначимо значення довжин дуг, які відповідають на кривій 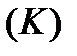 точкам
точкам 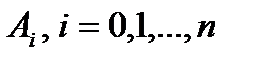 , через
, через  , тоді
, тоді
 .
.
Позначимо через 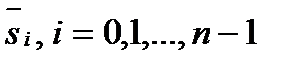 , значення довжини дуги, які визначають положення точок
, значення довжини дуги, які визначають положення точок 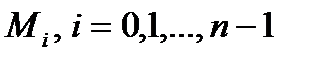
 . Тоді
. Тоді
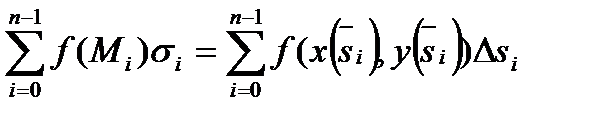 ,
,
тобто інтегральна сума для криволінійного інтеграла І роду є одночасно інтегральною сумою для звичайного визначеного інтегралу Римана, тому маємо:
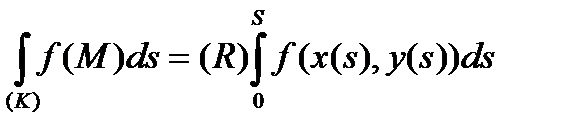 , (40)
, (40)
(де  означає звичайний інтеграл Римана), до того ж існування одного інтеграла веде за собою існування іншого.
означає звичайний інтеграл Римана), до того ж існування одного інтеграла веде за собою існування іншого.
Будемо далі припускати, що функція 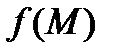 , яка визначена на кривій
, яка визначена на кривій  , є неперервною. Нехай тепер проста крива
, є неперервною. Нехай тепер проста крива 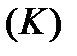 визначена довільними параметричними рівняннями:
визначена довільними параметричними рівняннями:
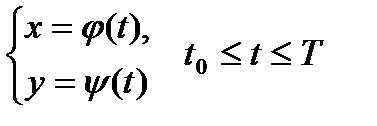 , (45)
, (45)
де функції  - неперервні. Тоді крива
- неперервні. Тоді крива  є спрямлюваною і, якщо зростання дуги
є спрямлюваною і, якщо зростання дуги  відповідає зростанню параметра
відповідає зростанню параметра 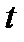 , то (як відомо з теми «Застосування інтеграла Римана»)
, то (як відомо з теми «Застосування інтеграла Римана»)
 . (50)
. (50)
Тоді

Таким чином, в випадку, коли крива  визначена параметрично за допомогою (45), формула зведення криволінійного інтегралу І типу до інтеграла Римана має вид:
визначена параметрично за допомогою (45), формула зведення криволінійного інтегралу І типу до інтеграла Римана має вид:
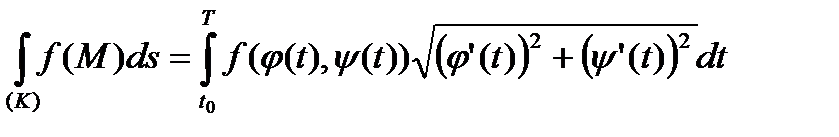 . (60)
. (60)
Нехай тепер крива  визначена за допомогою звичайного рівняння:
визначена за допомогою звичайного рівняння:
 , (70)
, (70)
тоді для того, щоб застосувати формулу (60) в цьому випадку, приведемо завдання кривої (70) до параметричного виду звичайним способом, розглядаючи змінну  як параметр:
як параметр:
 .
.
Формула (60) приймає вид:
 . (80)
. (80)
Приклад. Обчислити криволінійний інтеграл І типу  , де
, де  - це чверть еліпсу
- це чверть еліпсу 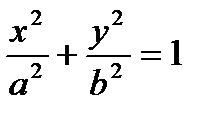 , яка знаходиться в І квадранті.
, яка знаходиться в І квадранті.
Перейдемо до параметричного завдання потрібної частки еліпсу:
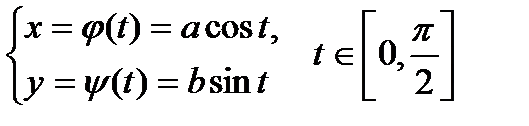 .
.
Тоді
 .
.
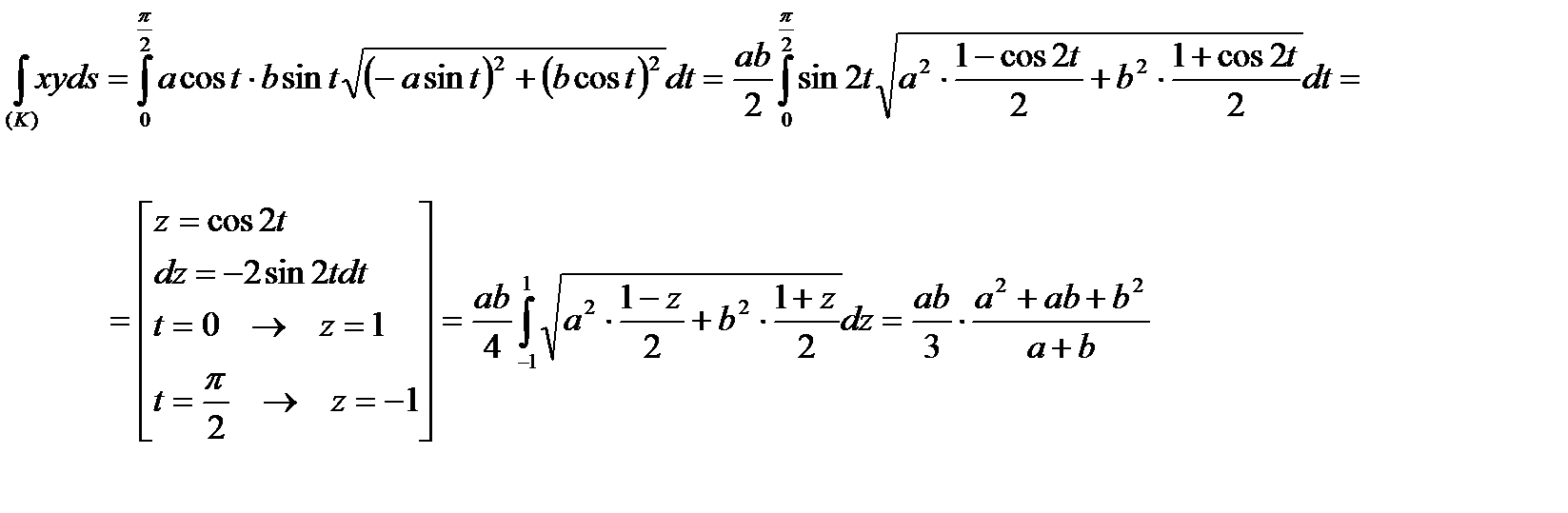
Питання
- Побудова інтегральної суми для криволінійного інтеграла І роду.
- Визначення криволінійного інтеграла І роду.
- Формула зведення криволінійного інтеграла І роду до інтеграла Римана у випадку, коли крива визначена параметрично.
- Формула зведення криволінійного інтеграла І роду до інтеграла Римана у випадку, коли крива визначена звичайним способом.
Дата добавления: 2015-08-21; просмотров: 1166;
