Задача про обчислення маси кривої

Лекція 41. Криволінійні інтеграли І роду

План

1. Задача про обчислення маси кривої
2. Визначення криволінійного інтегралу І роду
3. Зведення криволінійного інтегралу І роду до інтегралу Римана

Задача про обчислення маси кривої

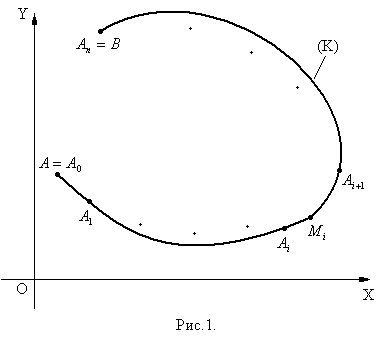
Нехай на площині задана неперервна проста спрямлювана крива 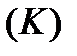деякої маси (рис.1), відома функція її лінійної густини 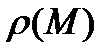у всіх точках кривої. Необхідно визначити масу 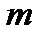всієї кривої .

Розіб’ємо криву 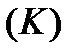на частки довільно обраними на ній проміжковими точками 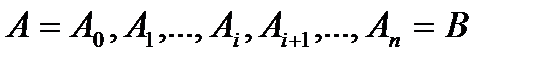(рис.1). Для визначеності будемо вважати, що точки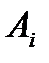

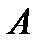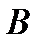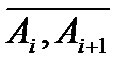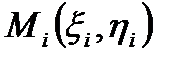занумеровані у напряму від до (але можливо і навпаки). На кожні частковій дузі оберемо довільно точку , з координатами (рис.1). Обчислимо в точках 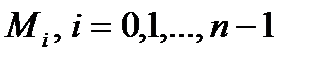, значення 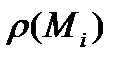. Будемо вважати, що в кожній точці часткової дуги 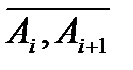така ж сама густина. Позначимо 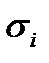довжину дуги 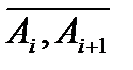. Тоді маса 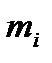часткової дуги 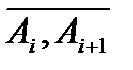буде оцінюватися як

,

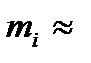
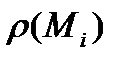
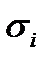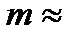
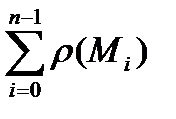
а 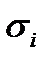. (10)

Якщо всі прямують до 0, то похибка для 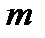, що обчислюється за допомогою формули (10), теж наближається до 0.

Нехай

,

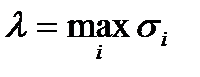тоді

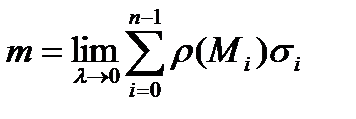. (20)

Розглянута задача дає наочне представлення про криволінійний інтеграл І роду.