Визначення криволінійного інтегралу І роду
Нехай вздовж кривої 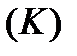 визначена якась функція
визначена якась функція 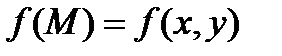 , яку назовемо «функцією точки». Повторимо дії, що були проведені вище для задачі про масу кривої для довільної функції
, яку назовемо «функцією точки». Повторимо дії, що були проведені вище для задачі про масу кривої для довільної функції 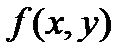 . Нехай
. Нехай 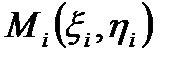
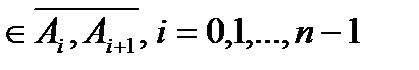 , побудуємо
, побудуємо
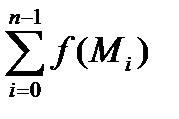
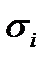 =
= 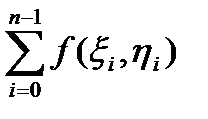
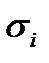 . (30)
. (30)
Сума (30) є інтегральною сумою для криволінійного інтегралу І типу.
Аналогічний процес побудови інтегральної суми можна використовувати і в випадку замкненої кривої.
Визначення 1. Нехай існує скінченна границя
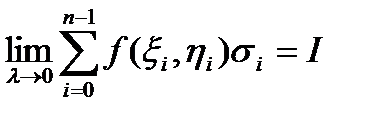 ,
,
яка не залежить ні від способу розбивки 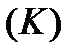 на частки
на частки 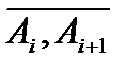 , ні від вибору проміжкових точок
, ні від вибору проміжкових точок 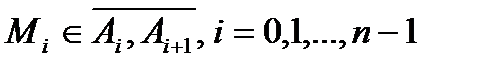 , то ця границя називається криволінійним інтегралом І роду від функції
, то ця границя називається криволінійним інтегралом І роду від функції 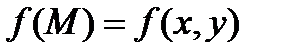 по кривій
по кривій 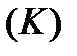 і позначається:
і позначається:
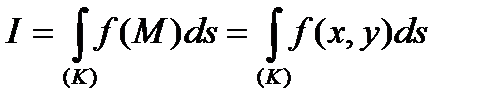 .
.
Тоді відповідно до формули (20) і визначення 1 маса кривої обчислюється як
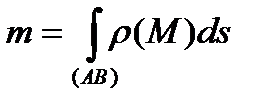 .
.
Зауваження 1. В визначенні криволінійного інтегралу І роду немає значення напрямок, який обирається на кривій 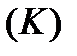 , тобто, якщо точки
, тобто, якщо точки 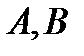 - це кінці кривої
- це кінці кривої 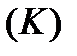 , то
, то
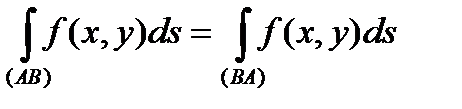 .
.
Аналогічно визначається криволінійний інтеграл І роду по кривій 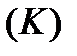 , яка знаходиться не на площині, а в тривимірному просторі:
, яка знаходиться не на площині, а в тривимірному просторі:
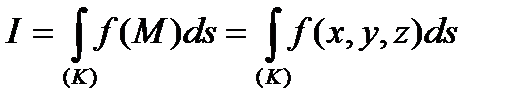 .
.
Дата добавления: 2015-08-21; просмотров: 1091;
